1. Overview
比特币利用了区块链技术,从发展和技术角度来理解比特币
2. 发展过程
2.1. 1 账本
基本规则
- 每个人都能向账本添加信息
- 月底统一结算
问题:添加信息时无法保证信息准确
2.2. 2 加密账本
使用数字加密技术,利用公钥+密钥,解决信用问题
- 产生的256位签名是根据内容和私钥,签名的验证是根据内容、签名和公钥
$$
Sign (Message, sk) = Signature
$$
比特币利用了区块链技术,从发展和技术角度来理解比特币
基本规则
问题:添加信息时无法保证信息准确
使用数字加密技术,利用公钥+密钥,解决信用问题
每次重装电脑都要重新安装Hexo的环境,步骤比较繁琐,所以记录下来方便之后再利用
1 | # 1.安装Nodejs和npm |
Prerequisite: A custom domain
设置步骤:
零空间、核,都描述的是一个东西
经过变换之后都变成零向量$\hat{0}$上的空间
也可以说是,已知变换矩阵$A$,求下面这个方程的解
$$
A\hat{x}=\hat{0}
$$
非方阵是升维或者降维
(编码器)+定子+转子+电刷+(减速器)
在电刷上施加直流电压U,施加洛伦兹力,不断重复
一般直流电机的转速都是一分钟几千上万转的,所以一般需要安装减速器。
减速器是一种相对精密的机械零件,使用它的目的是降低转速,增加转矩

编码器是将角位移或者角速度转换成一连串电数字脉冲的旋转式传感器
根据输出类型分类
过程控制、时序控制、运动控制都是控制,核心在于闭环反馈
掌握控制系统组成部件设备的基本原理和特性,能够选用合适的设备部件用于构成控制系统
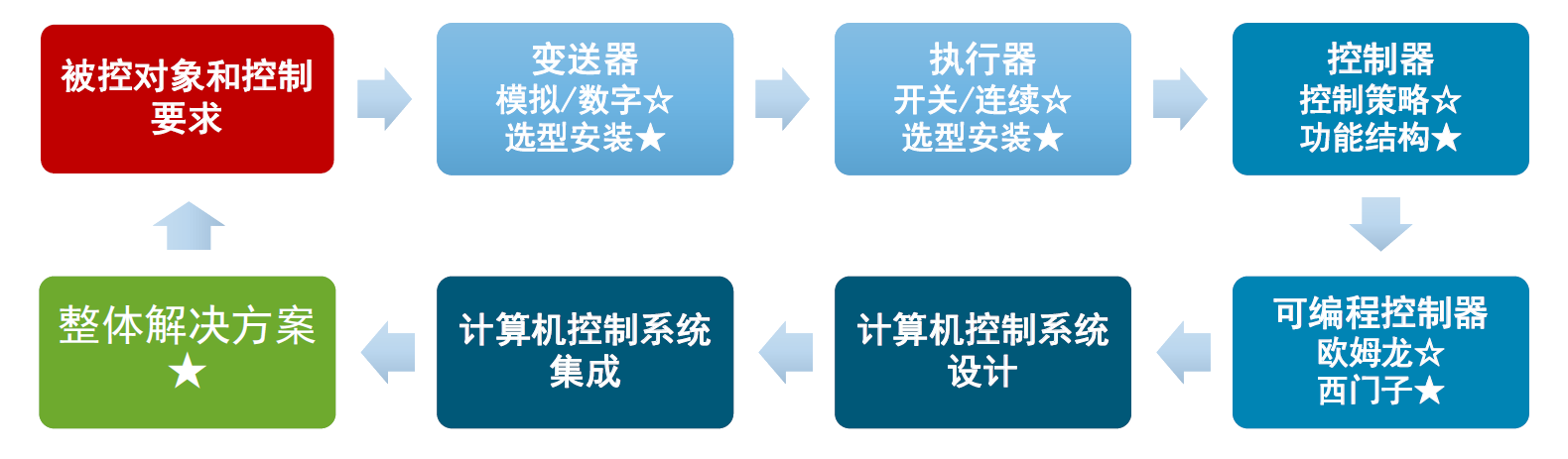
计算机体现在控制器的输入输出都是数字量的
FCS相当于DCS多一层级,把机柜下降到传感器的层级
基本概念
Do we have an obligation to obey laws?
Political Philosophy is examine philosophical questions about
State make demands to us
The **problem **is Why should we obey the laws
Note: $Obeying \not= Complying $
- Comply: do what the law commands, or they will be punished
- Obey: do what the law commands because the law commands it
We live with some sense of what is good or bad, better or worse.
So what is all the morality about?
Focus on the status of daily morality. , That is:
There are 3 theories :
This is a course note for the Introduction to Philosophy provided by University of Edinburgh hold on Coursera.
definition:
$the\ activity\ of\ working\ out\ the\ right\ way\ of\ thinking\ about\ things.$
So we need to stick in and do it to understand philosophy
we need to do philosophy by the challenges or results that other subjects throw up
e.g.
要想学会游泳,首先要克服的是自己的恐惧,不要害怕溺水,做好以下几步以防溺水
练习时要练习两种呼气
HTML means hyper text markup language
HTML的作用是定义网页的结构, 比如说哪一段是标题, 哪一段是文章内容, 哪一段是图片等, 就类似于MarkDown中定义了怎么样的是标题, 怎么样的是列表一样. 具体长什么样由CSS决定
1 | <p>My cat is very grumpy</p> |
由部分组成
3部分组合起来叫做element. element可以有一些属性attribute
1 | <!DOCTYPE html> |