1. Intro
$$
\begin{aligned}
& \int_{-\infty}^{\infty} \frac{\sin (x)}{x} \frac{\sin (x / 3)}{x / 3} \frac{\sin (x / 5)}{x / 5} \frac{\sin (x / 7)}{x / 7} \frac{\sin (x / 9)}{x / 9} d x=\pi \
& \int_{-\infty}^{\infty} \frac{\sin (x)}{x} \frac{\sin (x / 3)}{x / 3} \frac{\sin (x / 5)}{x / 5} \frac{\sin (x / 7)}{x / 7} \frac{\sin (x / 9)}{x / 9} \frac{\sin (x / 11)}{x / 11} d x=\pi \
& \int_{-\infty}^{\infty} \frac{\sin (x)}{x} \frac{\sin (x / 3)}{x / 3} \frac{\sin (x / 5)}{x / 5} \frac{\sin (x / 7)}{x / 7} \frac{\sin (x / 9)}{x / 9} \frac{\sin (x / 11)}{x / 11} \frac{\sin (x / 13)}{x / 13} d x=\pi \
& \int_{-\infty}^{\infty} \frac{\sin (x)}{x} \frac{\sin (x / 3)}{x / 3} \frac{\sin (x / 5)}{x / 5} \frac{\sin (x / 7)}{x / 7} \frac{\sin (x / 9)}{x / 9} \frac{\sin (x / 11)}{x / 11} \frac{\sin (x / 13)}{x / 13} \frac{\sin (x / 15)}{x / 15} d x=(0.99999999998529) \pi \
& \int_{-\infty}^{\infty} \frac{\sin (x)}{x} \frac{\sin (x / 3)}{x / 3} \frac{\sin (x / 5)}{x / 5} \frac{\sin (x / 7)}{x / 7} \frac{\sin (x / 9)}{x / 9} \frac{\sin (x / 11)}{x / 11} \frac{\sin (x / 13)}{x / 13} \frac{\sin (x / 15)}{x / 15} \frac{\sin (x / 17)}{x / 17} d x=(0.99999998807962) \pi
\end{aligned}
$$
Why?
2. Sliding Window
Moving average
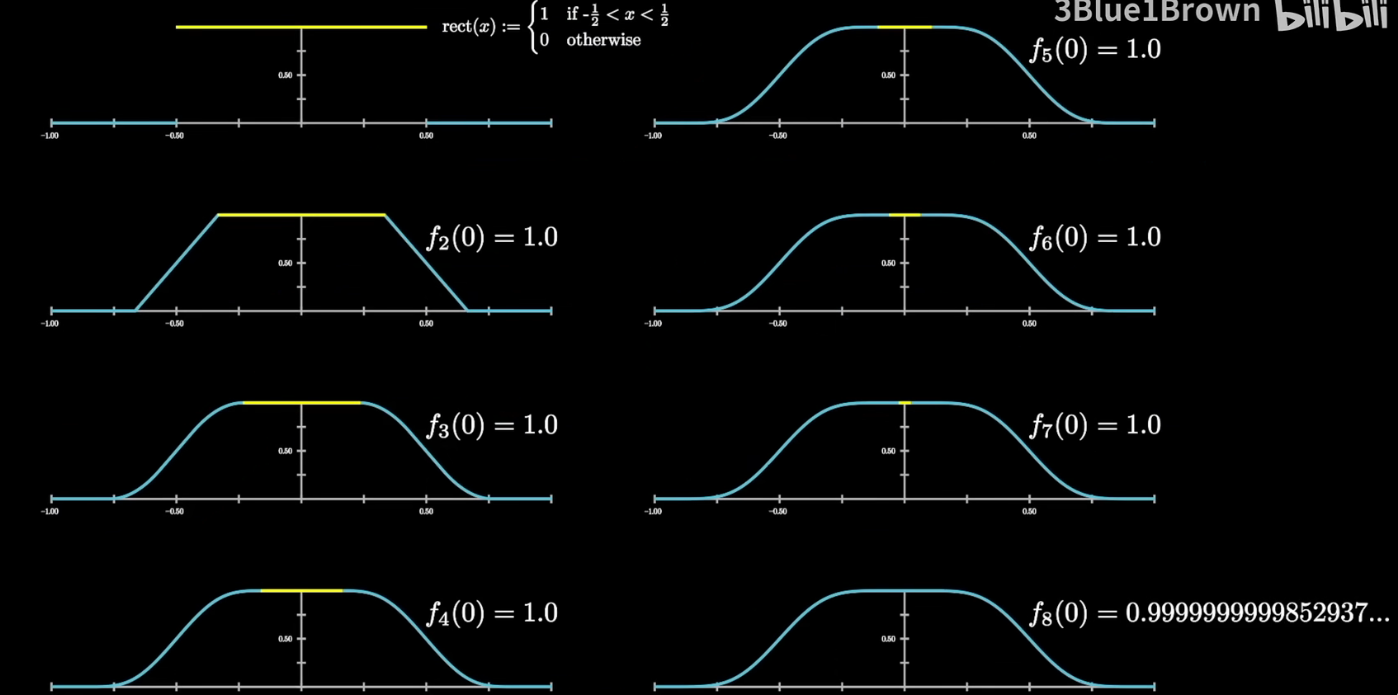
Same pattern
Stable for sometime, then change suddenly
3. Sinc function
$$
\int_{-\infty}^{\infty} \frac{\sin (\pi x)}{\pi x} d x=1.0
$$
Why
Since it’s the Fourier tranform of the rect function
$$
\int_{-\infty}^{\infty} f(t) d t=\mathcal{F}f(t)
$$
4. FT
$$
\mathcal{F}\left[\frac{\sin (\pi x)}{\pi x} \cdot \frac{\sin (\pi x / 2)}{\pi x / 2}\right]=\mathcal{F}\left[\frac{\sin (\pi x)}{\pi x}\right] * \mathcal{F}\left[\frac{\sin (\pi x / 2)}{\pi x / 2}\right]
$$
So just window average