1. Motivation
We want to decompose a matrix using an outer product of two vectors
2. SVD Singular Value Decomposition
2.1. Motivation
we except the topics to be orthogonal, so it can express most information
2.2. Idea
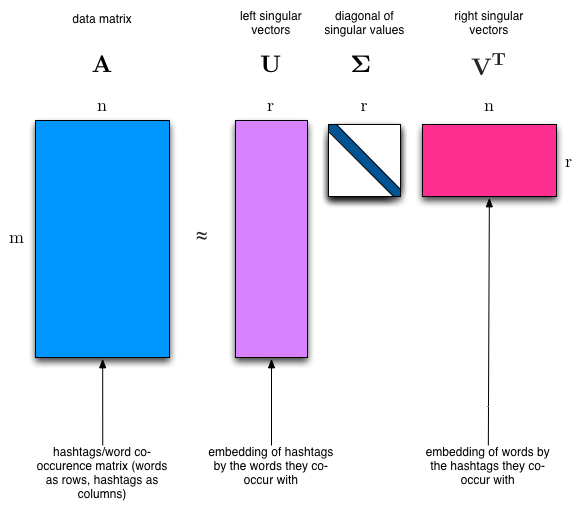
2.3. Application
- recommendation
- calculate pseudoinverse
- data compression
- PCA
3. NMF Non-negative Matrix Factorization
3.1. Motivation
It’s hard to explain face image while using PCA since there is negative value
So this method avoid negative value
Benefits: fast and easy to use
3.2. Idea
Deprecate orthogonal idea, another idea: constrain them to be non-negative
Goal: Do decomposition
$$
V \approx W H
$$
Approach: add penalty to punish negative elements, that means the result will be just a approximation, and not-unique
Using SGD(Stochastic Gradient Descent), add
3.3. Application
- Face decomposition
- bioinformatics
- Topic modeling
4. Faster SVD
4.1. Motivation
- Normal SVD is pretty slow, we need to speed it up
- Data are often missing or inaccurate
- Take advantage if GPUs
We are just interested in the largest singular values
So introduce randomized algorithms that
- more stable
- needed matrix-vector products can be done in parallel
- performance guaranteed
4.2. Idea
Use a smaller matrix
Before: calculate SVD of $A(m\times n)$
Basic Math: Johnson-Lindenstrauss Lemma
a small set of points in a high-dimensional space can be embedded into a space of much lower dimension in such a way that distances between the points are nearly preserved.
- After: calculate SCD of $B(m,r)=AQ\space,\space r<<n$
4.3. Computation
- Find an approximation $Q$ to the range of $A$, here range means linear combination.
That means $Q$ has similar column space with $A$ but fewer columns
$$
A\approx Q Q^tA
$$
Construct $B=Q^TA$, which is small
Compute the SVD of $B=S \Sigma V^{T}$
Since $A\approx Q Q^T A=QB=QS \Sigma V^{T}$
if we set $U=QS$, we can get
$$
A\approx U\Sigma V^T
$$
- Done!
But how do we get $Q$ in step 1?
- Take a bunch of random vector $w_i$ and form a matrix $W$, in this way ,$AW$ represent the space that column of $A$ can span.
- Calculate $AW=QR$, where $Q$ form an orthonormal basis for $Aw$