1. Introduction
Top-down teaching method
Why study numerical linear algebra?
- important in computer science
4 things need consideration
- memory
- speed
- accuracy
- scalability
That means there will be trade-off while designing
2. Matrix Computations
mainly 2 type of computation
Matrix products
Matrix-Vector Products: e.g. Markov Chain, from one state to another state, there will be a probability matrix
Matrix-Matrix Products: e.g. calculate different situation
images can be represented by matrices
convolution
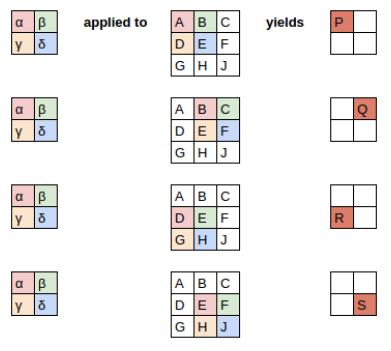
in matrix multiplication viewpoint

Matrix decompositions
Topic modeling: SVD, QR
Background removal: robust PCA, SVD
PageRank algorithm
3. Accuracy — How Computer Store Numbers
Why accuracy is a problem?
- Since computer store numbers finite and discrete
- Big problem while repeating an operation since each operation could multiply the error
Floats and doubles are not equidistant

Machine Epsilon: Half the distance between 1 and the next larger number
- defined by IEEE standards
- $\varepsilon_{\text {machine}}=2^{-53} \approx 1.11 \times 10^{-16}$
3.1. Conditioning and Stability
We need to know how small change in input will influence the output
“A stable algorithm gives nearly the right answer to nearly the right question.” –Trefethen
since we can not tell the computer the “right” number
Conditioning: perturbation behavior of a mathematical problem (e.g. least squares)
Stability: perturbation behavior of an algorithm used to solve that problem on a computer (e.g. least squares algorithms, householder, back substitution, gaussian elimination)
- e.g. while calculating eigen value, a small change in the input will get totally wrong answer
3.2. Approximation accuracy
Most of the time, we just don’t need to do highly matrix computations at scale,
- machine learning, more efficient
- Bloom filter algorithm, AdBlock, would give false positives, reduction in memory use of thousands of times
4. Memory Use – How Computer Store Matrices
A key way to save memory: just store the non-zero elements, this is called sparse storage. This is suited to sparse matrices that most elements are zero
The opposite, is dense storage, store every elements
5. Speed – How Computer Compute Matrices
Some key points to be considerd
- Computational complexity: the big O notation, algorithm
- Vectorization: Modern GPU and CPU, use low-level APIs: BLAS, LAPACK, hardware
- Scaling to multiple cores and nodes
- Locality: move data around, hardware
6. Scalability
Use multiple core and machine