1. 粒子滤波算法
2. 1 粒子滤波算法过程解析
粒子滤波定位算法的思想也是贝叶斯规则:
$$
\frac{\text { Likelihood * Prior }}{\text { Marginal }}
$$
以下的解析是结合Matlab代码所作的说明
- 初始化
- 初始化一堆粒子,在MatLab中的代码显示NP=50,也就是总共有50个采样粒子。Estimated State [x y yaw],可见每个状态有3个数据。px=repmat(xEst,1,NP);,
- 计算初始权重pw=zeros(1,NP)+1/NP; 可见初始权重是均匀的
- 初始化路标,landMarks=[10 0; 10 10; 0 15; -5 20]; 可见一共有4个路标
- 预测:根据motion model与物体的控制信息u预测下个时刻粒子群中粒子的位置
- doControl()函数,输入参数time,得到控制指令u
- doMotion()函数,输入初始状态x和控制指令u,得到下一时刻的x状态
- doObservation()函数,输入参数xGnd(没有噪声的里程计位置估计), xOdom(有噪声的里程计位置估计), u(控制指令), landMarks, MAX_RANGE,输出参数是z,xGnd,xOdom,u
- 更新:根据物体的观测值z与地图值zl计算出每个粒子的权重ww。更新粒子权重的依据是粒子的观测值与地图标志物相似度的高低,越高的话该粒子的权重越大
- 对每个粒子循环操作
- doMotion()函数,对每个采样粒子输入初始状态x和控制指令u,得到下一时刻的x状态,并加入干扰
- 计算权重,用各个路标距离的高斯概率相乘得到总概率
- 重采样:根据粒子的权重w重新采样粒子
3. 2 重要代码(Tasks)
3.1. 2.1 观测模型
1 | % do Observation model |
3.2. 2.2 运动模型
1 | % do Motion Model |
3.3. 2.3 高斯函数
1 | % Gauss function |
3.4. 2.4 粒子归一化
1 | % Normalization |
3.5. 2.5 重采样
1 | function [px,pw]=ResamplingStep(px,pw,NTh,NP) |
4. 3 参数对比实验
4.1. 3.1 NP数效果实验
| NP | 效果 | 运行时间 |
|---|---|---|
| 3 | 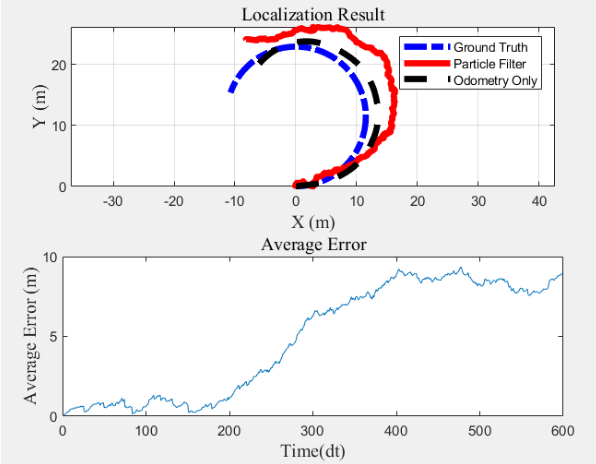 |
0.220 |
| 5 | !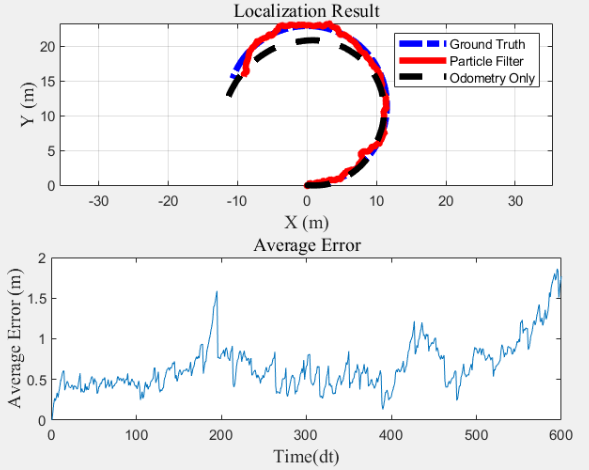 |
0.286 |
| 10 | 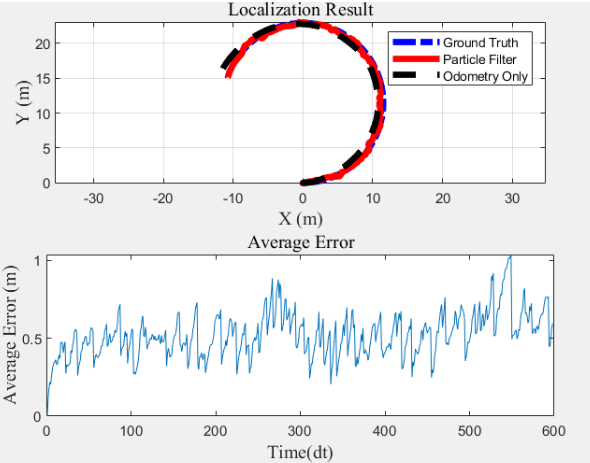 |
0.387 |
| 25 | 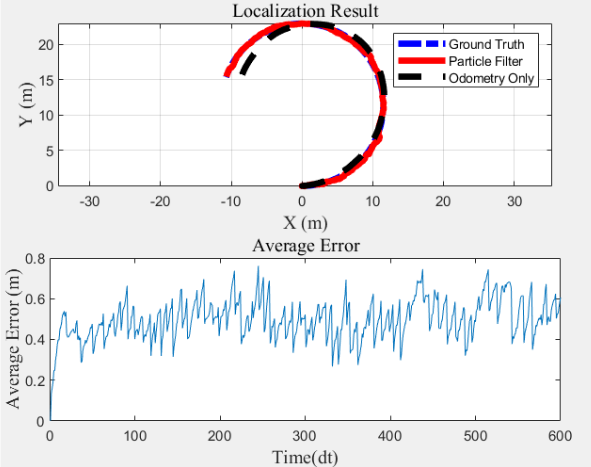 |
0.640 |
| 50 | 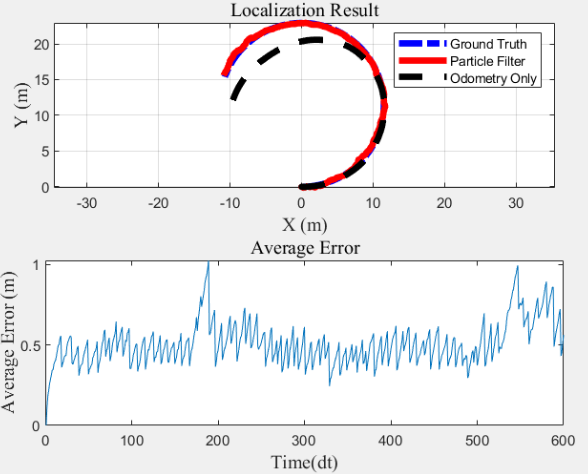 |
1.131 |
| 100 | 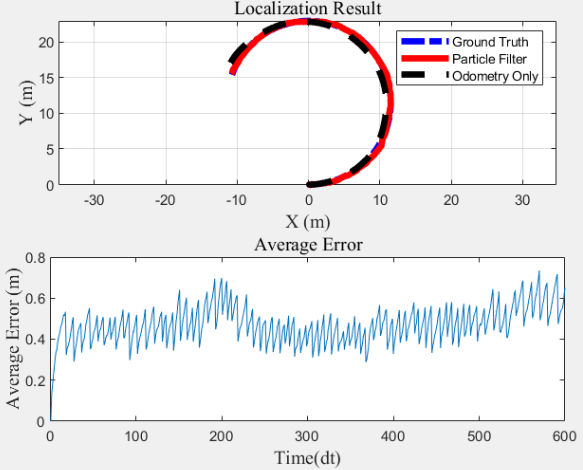 |
2.159 |
4.2. 3.2 NP数对时间的影响
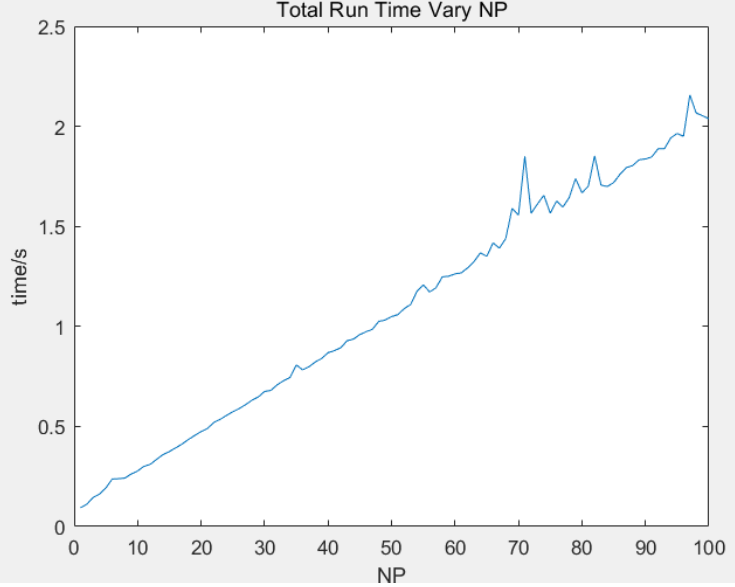
可见运行时间与NP数成正比关系
4.3. 3.3 NP数对误差的影响
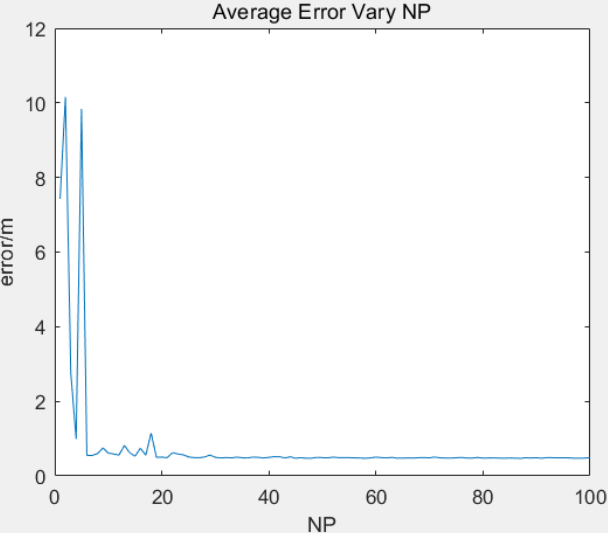
可见误差趋向于0.5,这主要时由高斯噪声造成的
5. 4 结论与展望
粒子滤波算法是基于概率的定位算法,主要有以下优点:
- 理解简单,一句话就是越相似,存活概率越大
- 计算量不大(计算量与粒子数线性相关)
但也存在以下问题:
- 严重依赖于对初始状态的估计,选择不当可能发散
- 需要有固定的路标
6. 参考文献
https://en.wikipedia.org/wiki/Particle_filter
[“Probabilistic Robotics”][Sebastian Thrun]