1. 1 视觉里程计:ICP
前端也称为视觉里程计(VO)。它根据相邻图像的信息,估计出粗略的相机运动,给后端提供较好的 初始值
1.1. 1.1 图像特征点
有代表性的点被称为
- 经典SLAM中:路标
- 视觉SLAM中:图像特征(features
特征点由两部分组成:
- 关键点:特征点在图像里的位置、朝向、大小
- 描述子:通常是一个向量,描述周围像素的信息
常见图像特征点:
- SIFT(Scale-Invariant Feature Transform):运算量大
- FAST:计算快
- ORB(Oriented FAST and Rotated BRIEF):折中
- 关键点为 FAST:如果一个像素与它领域的像素差别较大,则更可能是角点
- 描述子为 BRIEF:二进制描述子,关键点附近两个像素的大小关系
1.2. 1.2 对极几何:2D-2D
有了若干对匹配点,就可以通过对应关系,恢复出两帧之间的运动
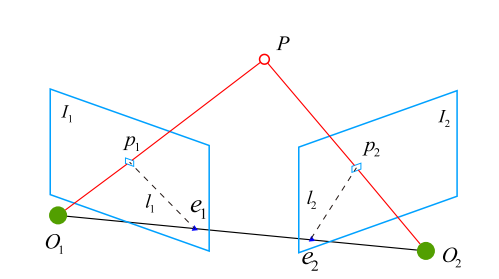
设$P$的空间位置为:$\boldsymbol{P}=[X, Y, Z]^{T}$
$p_1,p_2$的像素位置为$s_{1} \boldsymbol{p}{1}=\boldsymbol{K} \boldsymbol{P}, \quad s{2} \boldsymbol{p}_{2}=\boldsymbol{K}(\boldsymbol{R} \boldsymbol{P}+\boldsymbol{t})$ 其中$K$是相机内参矩阵
经过数学运算得到对极约束:$\boldsymbol{p}{2}^{T} \boldsymbol{K}^{-T} \boldsymbol{t}^{\wedge} \boldsymbol{R} \boldsymbol{K}^{-1} \boldsymbol{p}{1}=0$
几何意义是$O_1,P,O_2$三者共面
中间部分记作两个矩阵
本质矩阵$\boldsymbol{E}=\boldsymbol{t}^{\wedge} \boldsymbol{R}$
基础矩阵$\boldsymbol{F}=\boldsymbol{K}^{-T} \boldsymbol{E} \boldsymbol{K}^{-1}$
对极约束进一步化简为$\boldsymbol{x}{2}^{T} \boldsymbol{E} \boldsymbol{x}{1}=\boldsymbol{p}{2}^{T} \boldsymbol{F} \boldsymbol{p}{1}=0$
相机位姿估计问题抽象为
- 根据配对点和像素位置,求出$E$
- 根据$E$,求出$R,t$
1.3. 1.3 PnP问题:3D-2D
PnP(Perspective-n-Point),用在双目或RGB-D的视觉里程计使用
求解方法多样:
- 直接线性变换
- EPnP
- 非线性优化,构建最小二乘问题,Bundle Adjustment
1.4. 1.4 ICP问题:3D-3D
假设有一组配对好的3D点$\boldsymbol{P}=\left{\boldsymbol{p}{1}, \ldots, \boldsymbol{p}{n}\right}, \quad \boldsymbol{P}^{\prime}=\left{\boldsymbol{p}{1}^{\prime}, \ldots, \boldsymbol{p}{n}^{\prime}\right}$
要找的是欧式变换使得$\forall i, \boldsymbol{p}{i}=\boldsymbol{R} \boldsymbol{p}{i}^{\prime}+\boldsymbol{t}$
这个问题可以用迭代最近点(Iterative Closest Point, ICP)来解决,解决方法有
- 线性代数求解 SVD
- 定义误差项 $e_{i}=\boldsymbol{p}{i}-\left(\boldsymbol{R} \boldsymbol{p}{i}^{\prime}+\boldsymbol{t}\right)$
- 构建最小二乘问题$\min {\boldsymbol{R}, t} J=\frac{1}{2} \sum{i=1}^{n}\left|\left(\boldsymbol{p}{i}-\left(\boldsymbol{R} \boldsymbol{p}{i}^{\prime}+\boldsymbol{t}\right)\right)\right|_{2}^{2}$
- 可以化简为$\min {\boldsymbol{R}, \boldsymbol{t}} J=\frac{1}{2} \sum{i=1}\left|\boldsymbol{p}{i}-\boldsymbol{p}-\boldsymbol{R}\left(\boldsymbol{p}{i}^{\prime}-\boldsymbol{p}^{\prime}\right)\right|^{2}+\left|\boldsymbol{p}-\boldsymbol{R} \boldsymbol{p}^{\prime}-\boldsymbol{t}\right|^{2}$
- 发现左边项只和$R$有关,因此先求出$R$,令右边为$0$即可求出$t$
- 利用代码实现就是
- 求出两组点质心位置,求出去质心坐标
- 根据左边项求$\boldsymbol{R}^{*}=\arg \min {\boldsymbol{R}} \frac{1}{2} \sum{i=1}^{n}\left|\boldsymbol{q}{i}-\boldsymbol{R} \boldsymbol{q}{i}^{\prime}\right|^{2}$
- 求出$t$
- 非线性优化 BA
迭代求解
1.5. 1.5 三角化获得三维结构
2. 2 视觉里程计:直接法
使用特征点的方法有一些缺点:
- 就算是ORB算法也很耗时
- 图像上很多信息没有利用到
- 相机有时候会运动到特征确实的地方(面对着墙)
直接法就不匹配描述子,直接比较像素或特征点,有几种思路
- 光流法,使用特征点,只计算关键点,不计算描述子
- 直接法,只计算关键点,根据像素灰度信息来计算
总的来说,通过最小化光度误差来求解
2.1. 2.1 Lucas-Kanade 光流法
灰度是位置和时间的函数
$$
\boldsymbol{I}(x, y, t)
$$
光流法的基本假设:
灰度不变假设,同一空间点的像素灰度值,在各个图像中不变
$$
\boldsymbol{I}(x+\mathrm{d} x, y+\mathrm{d} y, t+\mathrm{d} t)=\boldsymbol{I}(x, y, t)=\boldsymbol{I}(x, y, t)+\frac{\partial \boldsymbol{I}}{\partial x} \mathrm{d} x+\frac{\partial \boldsymbol{I}}{\partial y} \mathrm{d} y+\frac{\partial \boldsymbol{I}}{\partial t} \mathrm{d} t
$$
所以
$$
\frac{\partial \boldsymbol{I}}{\partial x} \mathrm{d} x+\frac{\partial \boldsymbol{I}}{\partial y} \mathrm{d} y+\frac{\partial \boldsymbol{I}}{\partial t} \mathrm{d} t=0
$$
一个方程两个未知数,所以还需要一个假设某一个窗口内的像素具有相同的运动
如果选取一个$w\times w$的窗口,就有$w^2$个像素,也就有$w^2$个方程,还是两个未知数,就可以利用最小二乘来求解出速度$u,v$
3. 3 设计前端
3.1. 3.1 确定程序框架
选用RGB-D摄像头实现,因为较为简单,没有初始化,没有尺度问题。
建立不同的文件夹,分类存放文件
- bin 存放可执行的二进制
- include/slam 主要是.h头文件
- src 主要是.cpp源文件
- test 主要是.cpp测试源文件
- lib 编译好的库文件
- config 存放配置文件
- cmake_modules 第三方的cmake库
3.2. 3.2 基本类及其关系

3.3. 3.3 基本逻辑
3种状态
- 初始化:计算ORB,设定初始位姿
- 正常:计算ORB,特征匹配,位姿估计PnP,设定新位姿
- 特征匹配时使用hamming距离,找出所有匹配之间最大和最小
- 位姿估计时把匹配点转换为向量
- 丢失:跳过
4. 4 后端优化
状态估计
- Batch:批量的,状态估计会用未来的信息更新自己
- Incremental:渐进的,当前状态只有过去的时刻决定
希望:轨迹在较长时间内能保持最优
问题:只有里程计,会对自己的运动估计越来越不确定
sfm问题:从一组图像中恢复运动和结构
$$
P\left(\boldsymbol{x}{k} | \boldsymbol{x}{0}, \boldsymbol{u}{1 : k}, \boldsymbol{z}{1 : k-1}\right)=\int P\left(\boldsymbol{x}{k} | \boldsymbol{x}{k-1}, \boldsymbol{x}{0}, \boldsymbol{u}{1 : k}, \boldsymbol{z}{1 : k-1}\right) P\left(\boldsymbol{x}{k-1} | \boldsymbol{x}{0}, \boldsymbol{u}{1 : k}, \boldsymbol{z}{1 : k-1}\right) \mathrm{d} \boldsymbol{x}{k-1}
$$
4.1. 4.1 线性系统和KF
假设马尔可夫性,右侧第一部分中当前状态之和上一个时刻有关
$$
P\left(\boldsymbol{x}{k} | \boldsymbol{x}{k-1}, \boldsymbol{x}{0}, \boldsymbol{u}{1 : k}, \boldsymbol{z}{1 : k-1}\right)=P\left(\boldsymbol{x}{k} | \boldsymbol{x}{k-1}, \boldsymbol{u}{k}\right)
$$
右侧第二部分
$$
P\left(\boldsymbol{x}{k-1} | \boldsymbol{x}{0}, \boldsymbol{u}{1 : k}, \boldsymbol{z}{1 : k-1}\right)=P\left(\boldsymbol{x}{k-1} | \boldsymbol{x}{0}, \boldsymbol{u}{1 : k-1}, \boldsymbol{z}{1 : k-1}\right)
$$
高斯线性系统
$$
\left{\begin{array}{ll}{\boldsymbol{x}{k}=\boldsymbol{A}{k} \boldsymbol{x}{k-1}+\boldsymbol{u}{k}+\boldsymbol{w}{k}} \ {z{k}=\boldsymbol{C}{k} \boldsymbol{x}{k}+\boldsymbol{v}_{k}}\end{array} \quad k=1, \ldots, N\right.
$$
其中状态和噪声都满足高斯分布(零均值)
所以整个问题归纳为
已知:
- $k-1$时刻的后验状态估计:$\hat{\boldsymbol{x}}{k-1},\hat{\boldsymbol{P}}{k-1}$
- $k$时刻的输入和观测
求取:
- $x_k$的后验分布
后验均值的表达,就是两个步骤,预测和更新
预测
更新,计算$K$,成为卡尔曼增益
$$
\boldsymbol{K}=\overline{\boldsymbol{P}}{k} \boldsymbol{C}{k}^{T}\left(\boldsymbol{C}{k} \overline{\boldsymbol{P}}{k} \boldsymbol{C}_{k}^{T}+\boldsymbol{Q}\right)^{-1}
$$
卡尔曼滤波器构成了线性系统的最优无偏估计
4.2. 4.2 非线性系统和EKF
运动方程和观测方程一般是非线性函数,所以我们需要近似,近似成高斯分布
方式:线性化,就相当于一阶泰勒展开(求偏导)
仿照卡尔曼滤波,定义新的卡尔曼增益$K$
$$
\boldsymbol{K}{k}=\overline{\boldsymbol{P}}{k} \boldsymbol{H}^{\mathrm{T}}\left(\boldsymbol{H} \overline{\boldsymbol{P}}{k} \boldsymbol{H}^{\mathrm{T}}+\boldsymbol{Q}{k}\right)^{-1}
$$
利用卡尔曼增益,计算后验概率
局限
- 假设了马尔可夫性,所以无法做回环检测
- 仅做了一次线性化,而一阶泰勒展开不一定能够近似整个函数,只能在很小的范围内成立
- $EKF$存储了状态量的均值和方差
4.3. 4.3 非线性优化
Bundle Adjustment:从视觉重建中提炼出最优的3D模型和相机参数(内参,外参)
在以图优化框架的视觉SLAM问题中,BA起到了核心作用。求解只有观测方程的SLAM问题
SLAM问题中,BA具有稀疏特性,可以在实时场景中使用
4.3.1. 投影模型
从世界坐标系到像素坐标
- 世界坐标$\to$相机坐标,利用外参
$\boldsymbol{P}^{\prime}=\boldsymbol{R} \boldsymbol{p}+\boldsymbol{t}=\left[X^{\prime}, Y^{\prime}, Z^{\prime}\right]^{T}$
- 相机坐标$\to$ 归一化坐标
$\boldsymbol{P}{c}=\left[u{c}, v_{c}, 1\right]^{T}=\left[X^{\prime} / Z^{\prime}, Y^{\prime} / Z^{\prime}, 1\right]^{T}$
- 归一化坐标$\to$去畸变
$\left{\begin{array}{l}{u_{c}^{\prime}=u_{c}\left(1+k_{1} r_{c}^{2}+k_{2} r_{c}^{4}\right)} \ {v_{c}^{\prime}=v_{c}\left(1+k_{1} r_{c}^{2}+k_{2} r_{c}^{4}\right)}\end{array}\right.$
- 去畸变$\to$像素坐标,利用内参
$\left{\begin{array}{l}{u_{s}=f_{x} u_{c}^{\prime}+c_{x}} \ {v_{s}=f_{y} v_{c}^{\prime}+c_{y}}\end{array}\right.$
上面的投影模型可以说就是观测方程
可以抽象为$z=h(\boldsymbol{x}, \boldsymbol{y})$
- $z$ 是观测数据,像素坐标
- $x$ 是相机位姿,外参$R,t$
- $y$ 是路标,三维点$p$
考虑所有时刻的观测量,可以计算整体的代价函数
$$
\frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{n}\left|\boldsymbol{e}{i j}\right|^{2}=\frac{1}{2} \sum{i=1}^{m} \sum_{j=1}^{n}\left|\boldsymbol{z}{i j}-h\left(\boldsymbol{\xi}{i}, \boldsymbol{p}_{j}\right)\right|^{2}
$$
4.4. 4.4 Ceres实践
根本问题:最小化投影误差,也就是多个特征点的平均投影误差
$$
\begin{aligned} r(\boldsymbol{\xi}) &=\mathbf{p}^{\prime}-\mathbf{p}=\left(u^{\prime}, v^{\prime}\right)-(u, v) \end{aligned}
$$
回顾Ceres,要做优化问题
- 构建代价函数
- 使用自动求导,需要构造代价函数结构体,对模板括号
()重载,定义残差,()中前几个是待优化变量,最后一个是残差 - 模板参数
<>中第一个参数代价函数结构体的名字,然后是残差的维度,后几个为待优化状态量的维度 - 用代价函数,待优化变量构建优化问题
- 配置求解器
- 运行求解器
5. 5 图优化
5.1. 5.1 位姿图 Pose Graph
采用之前的BA优化,时间越长,运动轨迹越长,地图规模也会增长,所以计算效率就会逐渐下降。如何解决这些问题?
考虑到在BA优化中,一些特征点会收敛至一个值保持不动,所以不需要再进行优化。
可以构建一个只有轨迹的图优化,而位姿节点之间的边,可以由两个关键帧之间通过特征 匹配之后得到的运动估计来给定初始值。不同的是,一旦初始估计完成,我们就不再优化 那些路标点的位置,而只关心所有的相机位姿之间的联系了。通过这种方式,我们省去了大 量的特征点优化的计算,只保留了关键帧的轨迹,从而构建了所谓的位姿图(Pose Graph)
6. 6 回环检测
6.1. 概述
前端:特征点提取,提供轨迹和地图的初值
后端:对前端提供的数据进行优化
但是只考虑相邻帧之间的位移,长期来看还是会有累计误差,所以要加入回环检测
所以仅有前端和局部后端的系统称为VO,而有回环检测和全局后端的称为SLAM
6.2. 实现
最简单的方式:任意两张做特征匹配,匹配多的关系就越强,但是计算量太大
几何的方式:在几何关系上回到起点时做检测,但是逻辑上也是鸡和蛋的问题
实际中应用的方式:基于外观,计算图像间的相似性
有两个统计量来检验判断效果
- 准确率,就是所有检测到的回环中是真实回环的概率,在SLAM中更加重要一些
- 召回率,就是所有真实回环中被检测到的概率
6.3. 词袋模型
Bag of Words (BoW),用图像特征来描述图像,比如说一张图片里两个人,另一张一个人
- 确定”人“的概念,相当于Words,许多Words组合在一起组成字典Dictionary
- 计算一张图中的各个Words,只计算出现的次数,和空间位置等无关
- 比较相似程度
字典的定义——通过聚类解决
问题抽象:从一张图片中提取了$N$个特征点,想要找一个有$k$