1. 1 前言
全书分为两部分
- 数学基础,涉及到SLAM概述、矩阵知识、李群知识、非线性优化
- SLAM技术,实践视觉里程计(特征点法、直接法),后端优化,回环检测
2. 2 SLAM概述
2.1. 2.1 SLAM框架各模块及任务
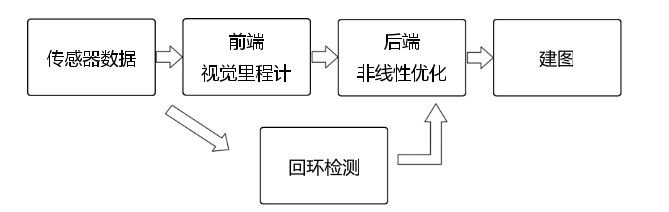
- VO:视觉里程计,和计算机视觉研究领域相关。根据两张图片确定旋转了多少度、平移了多少厘米。通过VO计算两帧之间的移动,再累加。问题是会有累计漂移,需要后端优化和回环检测
- 后端优化:降噪,估计整个系统的状态。主要是滤波和非线性优化算法,优化轨迹
- 回环检测:解决累计漂移问题,让机器人具有识别曾经到达过的场景的能力
- 建图,现在常用的是度量地图,拓扑地图有待研究
- 稀疏:仅表达重要物体,即路标,对定位来说,稀疏地图就够了
- 稠密:建模所有东西,用于导航ls
2.2. 2.2 编程环境
Ubuntu14.04
CMake
g++
2.3. 2.3 库
C++工程中,只有带main函数的文件才会生成可执行程序,另外的代码供其他程序应用。叫做库
- 静态库:.a作为后缀名,每次被调用都会产生一个副本
- 共享库:.so作为后缀名,只有一个副本,更省空间
一个库往往是许多算法、程序的集合。如果只有二进制库,不方便使用,所以提供头文件,方便调用。
如果可执行程序想要调用库中的函数,需要参考头文件,并把可执行程序链接到库文件上。
2.4. 2.4 cmake基本用法
cmake处理了工程文件之间的关系,make调用g++编译程序
所以维护CMakeLists.txt降低了维护难度
3. 3 三维空间刚体运动
3.1. 3.1 运动描述方式
旋转矩阵$S O(n)$是特殊正交群的意思(Special Orthogonal Group),定义如下
$$
S O(n)=\left{\boldsymbol{R} \in \mathbb{R}^{n \times n} | \boldsymbol{R} \boldsymbol{R}^{T}=\boldsymbol{I}, \operatorname{det}(\boldsymbol{R})=1\right}
$$
$$
\boldsymbol{R}^{-1}=\boldsymbol{R}^T
$$
可以用来描述相机的旋转
如果是旋转加上平移,那就要用$SE(n)$来表示,意思是特殊欧式群(Special Euclidean Group),定义如下
$$
S E(3)=\left{T=\left[ \begin{array}{cc}{\boldsymbol{R}} & {\boldsymbol{t}} \ {\mathbf{0}^{T}} & {1}\end{array}\right] \in \mathbb{R}^{4 \times 4} | \boldsymbol{R} \in S O(3), \boldsymbol{t} \in \mathbb{R}^{3}\right}
$$
$$
\boldsymbol{T}^{-1}=\left[ \begin{array}{cc}{\boldsymbol{R}^{T}} & {-\boldsymbol{R}^{T} \boldsymbol{t}} \ {\mathbf{0}^{T}} & {1}\end{array}\right]
$$
上述的表示方法缺点是有冗余的变量表达,且旋转矩阵自身带有约束
改进:用2个三维向量表示
- 一个是旋转向量,方向与旋转轴一致,长度与旋转角一直
旋转向量和旋转矩阵的转换由罗德里格斯公式表明
- 另一个是平移向量
旋转向量对人来说不好理解,所以可以用欧拉角来表示,但是欧拉角表示会存在万向节死锁问题。
虽然旋转向量和欧拉角都是紧凑的,但是具有奇异性
因此引入四元数,类似于表示三维空间旋转的复数
3.2. 3.2 Eigen库使用
4. 4 李群与李代数
知道了三维空间中刚体的运动方式,而我们需要解决什么样的相机位姿最符合当前观测数据这样的问题,可以抽象为一个优化问题,求解最优的$R,t$,使得误差最小化
4.1. 4.1 基本概念
对于只有一个运算(比如$*$)的集合,我们把它叫做群,也就是说群是定义在一种集合加上一种运算的基础上的,比如$SO(n),SE(n)$
李群是指具有连续(光滑)性质的群,$SO(n),SE(n)$
李代数描述了李群的局部性质
李群通过对数映射得到李代数
李代数通过指数映射得到李群
4.2. 4.2 BCH近似
使用李代数的动机是为了优化
对李代数来说$\ln (\exp (\boldsymbol{A}) \exp(\boldsymbol{B}))=\boldsymbol{A}+\boldsymbol{B}$ 在矩阵时不成立
因此使用BCH(Baker-Campbell-Hausdorff)近似
4.3. 4.3 扰动模型
4.4. 4.4 Sophus对李代数的运算
MSVC中没有M_PI,需要增加
5. 5 相机与图像
5.1. 5.1 相机模型
5.1.1. 5.1.1 针孔相机模型
内参数:针孔模型+畸变模型
这两个模型把外部三维点投影到相机内部成像平面
5.1.2. 5.1.2 双目相机模型
利用视差计算像素深度
5.1.3. 5.1.3 RGB-D相机模型
主动测量每个像素的深度
- 通过结构光,比如Kinect 1,realsense
- 通过飞行时间法ToF,比如Kinect 2,原理类似于激光
5.2. 5.2 空间点如何投影到相机
5.3. 5.3 OpenCV中的图像存储与表示
宽度640,高度480的灰度图像,可以这样表示
1 | unsigned char image[480][640] |
因为第一个下标表示行,第二个下标表示列。
这样表示的原因是OpenCV中的图像也是矩阵,矩阵的数值选取是左上角原点,先纵再横。OpenCV规定纵是Y,横是X,所以最后是这样的表示
5.4. 5.4 摄像头标定
6. 6 非线性优化
之前已经说明了运动方程和观测方程,但是由于噪声的存在,所以要根据有噪声的数据进行状态估计。也就是要求一个最大似然估计或者最大后验概率,“在什么情况下最可能产生现在观测到的数据”
原来的观测模型加上高斯分布的噪声后,任然是高斯分布,所以我们可以使用最小化负对数来求高斯分布最大似然,这也等价于最小化噪声项,所以问题就抽象为最小二乘问题
6.1. 6.1 非线性最小二乘法
6.2. 6.2 下降策略
G-N 高斯牛顿法
L-M
6.3. 6.3 库的使用
6.3.1. 6.3.1 Ceres
Ceres——通用的优化库,从损失函数来理解比较自然
最小二乘问题的一般形式
$$
\min {x} \frac{1}{2} \sum{i} \rho_{i}\left(\left|f_{i}\left(x_{i_{1}}, \ldots x_{i_{n}}\right)\right|^{2}\right)
$$
在Ceres中,定义优化变量$x$和代价函数$f_i$,调用Ceres求解
方法:
- 定义损失函数的模型,就是一个类,并在类中定义带模板参数的
()运算符,使该类成为一个拟函数,使Ceres可以像调用函数一样调用这个类的对象 - 调用$AddResidualBlock$添加误差项成为目标函数,梯度我们可以
- Ceres的自动求导
- 数值求导
- 自行推导解析的导数形式,提供给Ceres
- 自动求导需要指定误差项和优化变量的维度
- 误差是标量,维度就是1
- 有3个参数要优化,维度就是3
6.3.2. 6.3.2 G2O
$g^2o$——基于图的优化库,需要定义新的顶点和边,但$g^2o$提供了很多顶点和边的类型,所以在相机位姿估计问题中非常方便,如果用Ceres,要自己实现损失函数,不方便。