基于几何关系的相机位姿估计

1. 1 问题描述

根据射影几何，真实世界中的圆在理想相机模型中的投影是一个椭圆。本文就是根据圆的半径和相机拍摄到的椭圆方程推导求解相机相对于圆心的位姿关系。为了简化问题，目前只考虑相机在一个角度的旋转$\beta$和位移$\Delta_l$

2. 2 关系图

如图所示，符号规定：

$d$: 正圆圆心到相机平面的距离

$f$: 相机的焦距

$Δc_2$: 圆心在成像平面的位移距离

$L_1$: 成像平面的椭圆的半径（与旋转平面垂直）

成像平面椭圆的半径可以看成是世界中正圆半径的缩放，缩放的比例只和到圆的距离有关。在距离不变的情况下，$L_1$是所对应的半径没有变化的那条半径

$L_2$: 成像平面的椭圆的半径（另一条）

$L$: 正圆的半径

$\beta$: 旋转的角度

2.1. 2.1 原点右侧几何关系

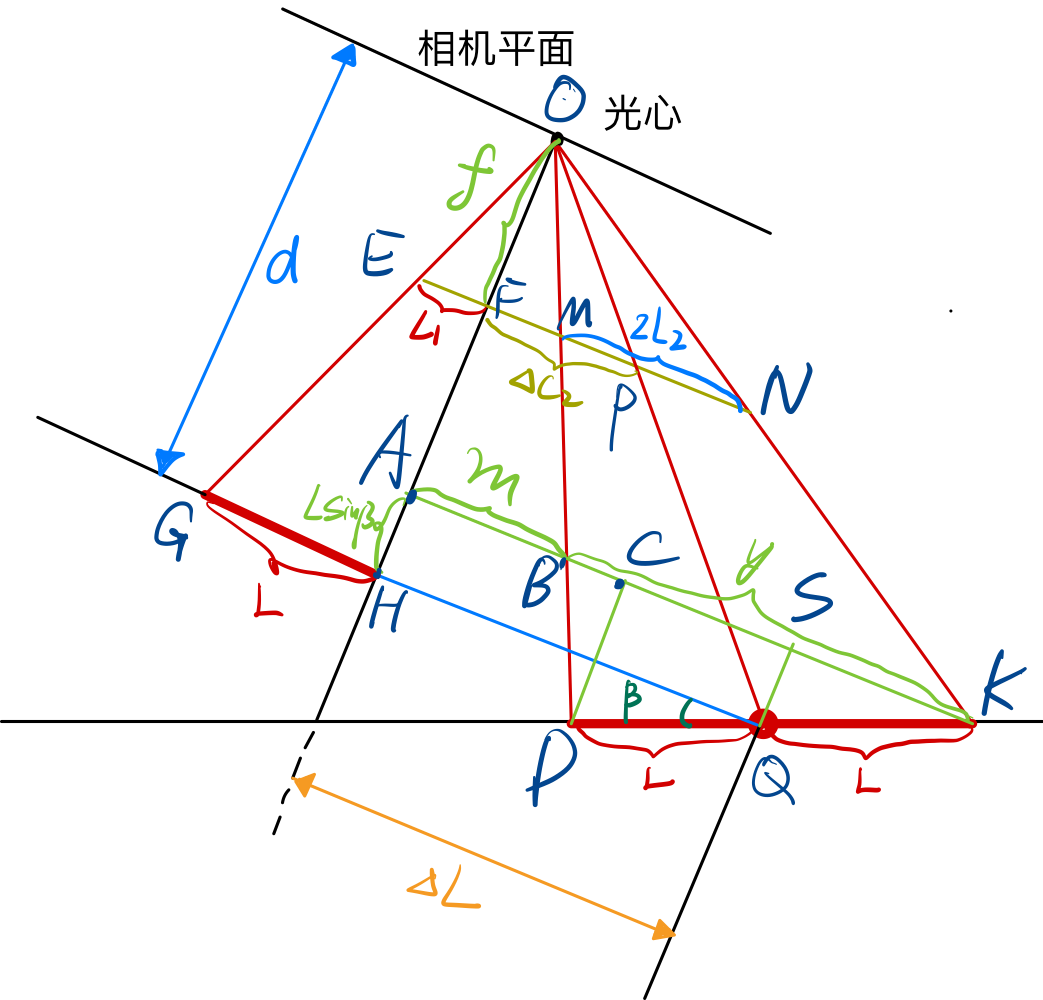
为了方便求解，增加辅助线，分别根据以下几何关系：

$\Delta OEF\sim \Delta OGH$
$\Delta OFP\sim \Delta OHQ$
$AB+BK=AS+SK$
$\Delta OMN\sim \Delta OBK$
$\Delta OBA \sim \Delta DBC$

可以得到以下关系
$$
\frac{f}{d}=\frac{L_{1}}{L}
$$

$$
\frac{f}{d}=\frac{\Delta C_{2}}{\Delta L}
$$

$$
m+y=\Delta L+L \cos \beta
$$

$$
\frac{2 L_{2}}{y}=\frac{f}{d-L \sin \beta}
$$

$$
\frac{m}{d-L \sin \beta}=\frac{y-2 L \cos \beta}{2 L \sin \beta}
$$

2.2. 2.2 原点左侧几何关系

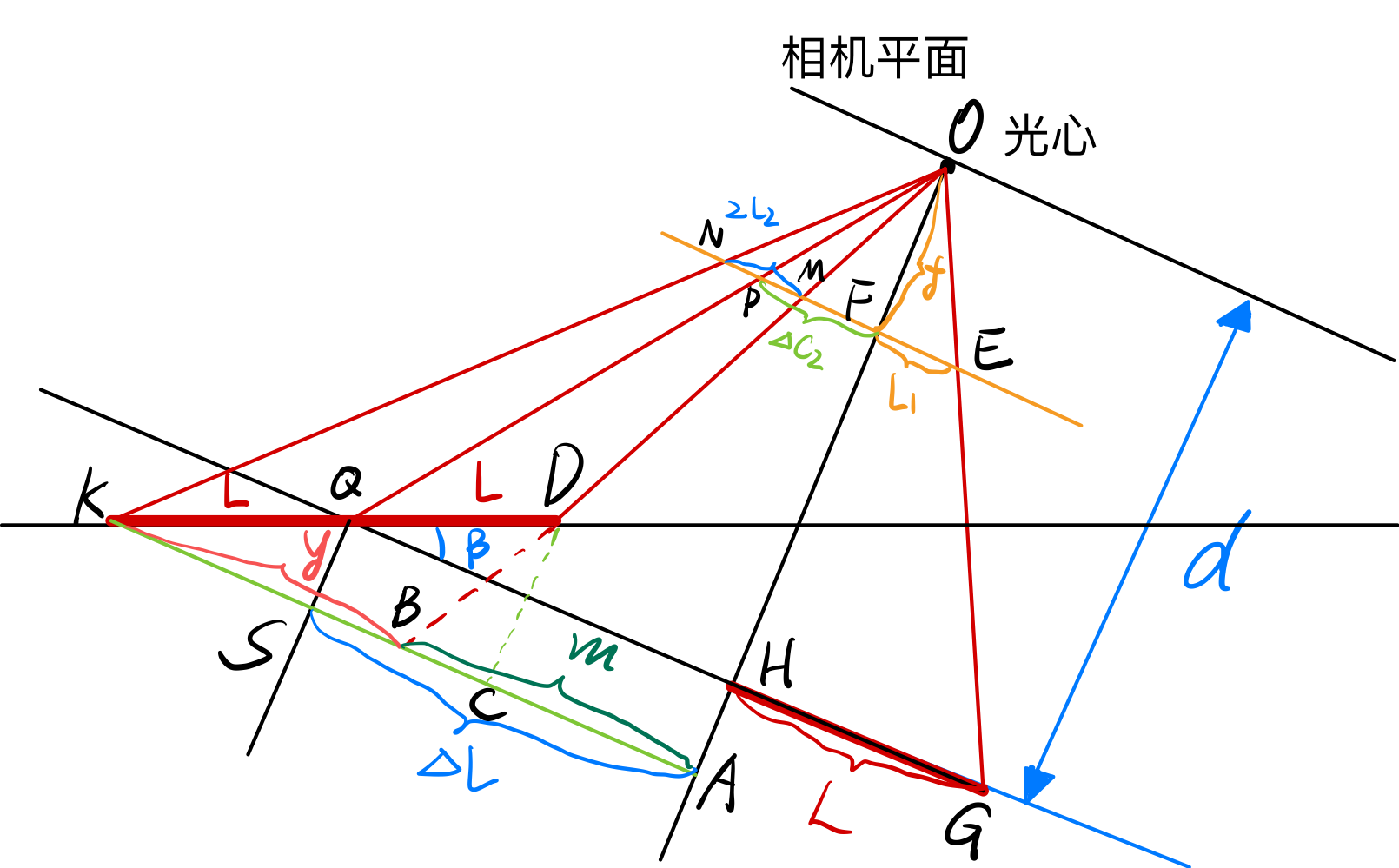
基于和2.1中一样的几何关系，

可以列出以下等式
$$
\frac{f}{d}=\frac{L_{1}}{L}
$$

$$
\frac{f}{d}=\frac{\Delta C_{2}}{\Delta L}
$$

$$
m+y=\Delta L+L \cos \beta
$$

$$
\frac{2 L_{2}}{y}=\frac{f}{d+L \sin \beta}
$$

$$
\frac{m}{d-L \sin \beta}=\frac{-(y-2 L \cos \beta)}{2 L \sin \beta}
$$

注意到上图中$\beta$定义的方向与2.1中相反，因此本质上两种情况是一样的

3. 3 方程求解推

3.1. 3.1 化简方程式

化简1、2、3、4可得

$$
d=\frac{fl}{L_1}
$$
$$
\Delta l=\frac{d \Delta C_{2}}{f}
$$

$$
m=\Delta L+L \cos \beta-y
$$
$$
y=\frac{2 L_{2}\left(d_{1}-L \sin \beta\right)}{f}
$$

将13带入5得到
$$
2 L \sin \beta(\Delta L+L \cos \beta-y)=(d-L \sin \beta) （ y-2 L \cos \beta)
$$
展开移项得到
$$
2 L \sin \beta(\Delta L+L \cos \beta)+2 L \cos \beta\left(d_{1}-L \sin \beta\right)=(d+L\sin \beta) y
$$
将14带入16得到
$$
2 L \Delta \sin \beta+2 L d \cos \beta=\frac{2 l_{2}}{f}\left(d^{2}-L^{2} \sin ^{2} \beta\right)
$$
展开移项得到
$$
f L d \cos \beta=L_{2} d^{2}-L_{2} L^{2} \sin ^{2} \beta-f L \Delta L \sin \beta
$$

将12带入18得到

$$
f L d \cos \beta=L_{2} d^{2}-L_{2} l^{2} \sin ^{2} \beta-d \Delta c_{2} L \sin \beta
$$
两边同时除d
$$
f L \cos \beta=L_{2} d-\frac{L_{2} L^{2} \sin \beta}{d}-\Delta c_{2} L \sin \beta
$$
将11带入20得到
$$
fL \cos \beta=\frac{L_{2} f L}{L_{1}}-\frac{L_{2} L^{2} L_{1} \sin ^{2} \beta}{f L}-\Delta c_{2} L \sin ^{2} \beta
$$

两边同时除$fL$
$$
\cos \beta=\frac{L_{2}}{L_{1}}-\frac{L_{1} L_{2} \sin^{2} \beta}{f^{2}}-\frac{\Delta c_{2} \sin \beta}{f}
$$

3.2. 3.2 一元四次方程

为了去掉分母，22两边同时乘$f^2L_1$
$$
f^2L_1\cos\beta=f^2L_2-L_1^2L_2\sin^2\beta-fL_1\Delta c_2\sin\beta
$$
得到17后，为了求解方程，两边同时平方，并设
$$
x=\sin \beta
$$
则
$$
x^2=\sin^2\beta
$$

$$
1-x^2=\cos^2\beta
$$

展开得到
$$
{L_1 }^2 ,f^4 ,({1-x^2)}={\Delta }^2 ,{L_1 }^2 ,f^2 ,x^2 +2,\Delta{c_2} ,{L_1 }^3 ,L_2 ,f,x^3 -2,\Delta{c_2} ,L_1 ,L_2 ,f^3 ,x+{L_1 }^4 ,{L_2 }^2 ,x^4 -2,{L_1 }^2 ,{L_2 }^2 ,f^2 ,x^2 +{L_2 }^2 ,f^4
$$

合并同类项，得到
$$
{\left({L_1 }^4 ,{L_2 }^2 \right)},x^4 +{\left(2,\Delta{c_2} ,{L_1 }^3 ,L_2 ,f\right)},x^3 +{\left({\Delta{c_2} }^2 ,{L_1 }^2 ,f^2 -2,{L_1 }^2 ,{L_2 }^2 ,f^2 +{L_1 }^2 ,f^4 \right)},x^2 +{\left(-2,\Delta{c_2} ,L_1 ,L_2 ,f^3 \right)},x+{L_2 }^2 ,f^4 -{L_1 }^2 ,f^4=0
$$

28本质上就是一个一元四次方程
$$
Ax^4+Bx^3+Cx^2+Dx+E=0
$$
其中

$$
A={L_1 }^4 {L_2 }^2
$$

$$
B={2,\Delta{c_2} ,{L_1 }^3 ,L_2 ,f}
$$

$$
C={ { \Delta{c_2} }^2 ,{L_1 }^2 ,f^2 -2,{L_1 }^2 ,{L_2 }^2 ,f^2 +{L_1 }^2 ,f^4 }
$$

$$
D={-2,\Delta{c_2} ,L_1 ,L_2 ,f^3 }
$$

$$
E={ {L_2 }^2 ,f^4 -{L_1 }^2 ,f^4}
$$

求解四次方程的解析解可以通过费拉里方法求解

4. 4 代码

def calculate_pitch_deltal(l1,l2,delta_c1, delta_c2, l_meter):
## Set the parameters
# definition:
#l1, perpendicular to conveyor belt, i.e., along y direction, the measured value of the eclipse,unit is meter and calculated as l1=ly_pixel*mu
#l2, parelled to conveyor belt,i.e., along x direction, the measured value of the eclipse, unit is meter and calculated as l2=lx_pixel*mu
#unit for l1,l2,delta_c1, delta_c2 are all lx_pixel

mu = 3.45*1e-6
f = 1024 # focal length
d_meter = f*l_meter/(l1)
delta_lx_meter = d_meter*delta_c2/f
delta_ly_meter = d_meter*delta_c1/f

## Calculate the coefficients
A = l1**4*l2**2
B = 2*delta_c2*f*l1**3*l2
C = delta_c2**2*f**2*l1**2+f**4*l1**2-2*f**2*l1**2*l2**2
D = -2*delta_c2*f**3*l1*l2
E = f**4*l2**2-f**4*l1**2
ans = ferrari(A,B,C,D,E)
potential_ans=[]
for a in ans:
if a.imag == 0:
x = a.real
beta = math.asin(x)/math.pi*180
potential_ans.append(beta)

# calculate delta lx that parelled to conveyor belt.
potential_move=[]
delta_l=d_meter*delta_c2/f
for beta in potential_ans:
beta_rad=beta/180*math.pi
delta_l_conveyor=(d_meter*math.tan(beta_rad)-delta_l)*math.cos(beta_rad)
potential_move.append(delta_l_conveyor)
return [d_meter,delta_lx_meter,delta_ly_meter, potential_ans]

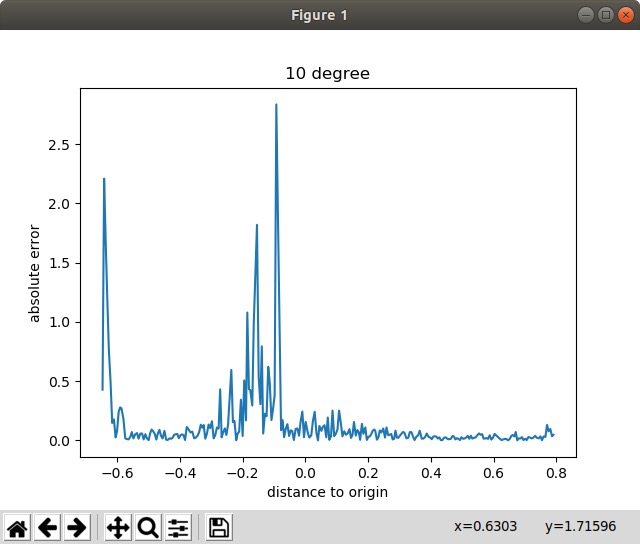
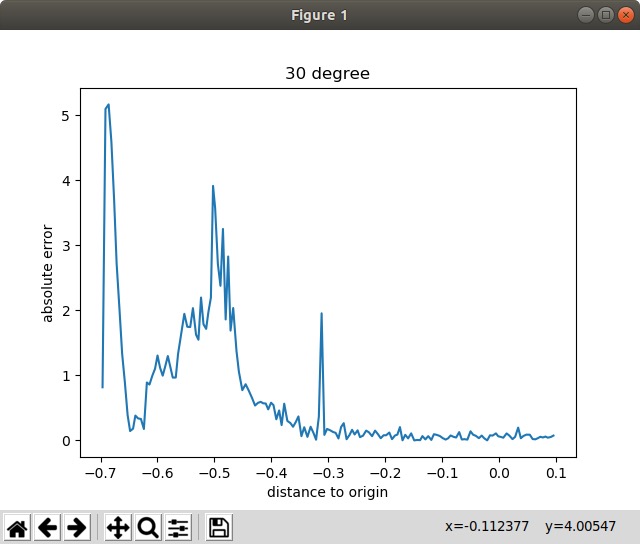
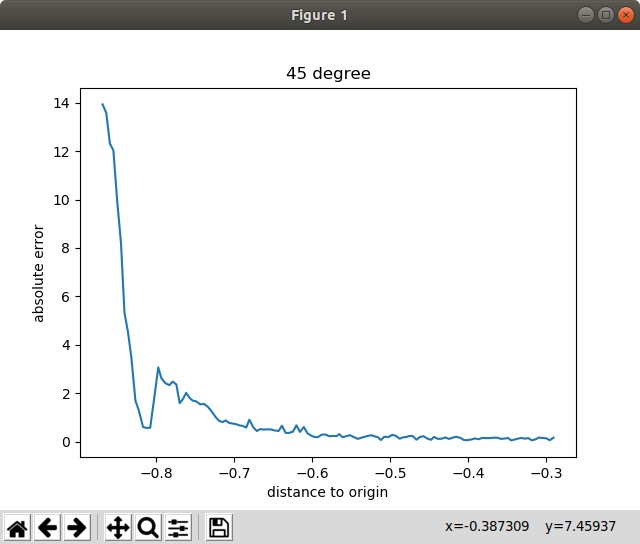
5. 5 实验验证

为了验证模型效果，在仿真中进行实验，改变相机的倾斜角度，让元件从传送带的远端逐渐接近相机

测试了3个角度（10度、30度、45度），分别计算了计算值与真值的误差