1. Intro
什么是SIFT?Scale Invariant Feature Transform
对下列变化不敏感
- 尺度变换
- 旋转
- 光照
- 视角
SIFT算法较为复杂,主要分为两个大的部分
- 找出特征点
- 目的是去掉一些不重要的细节。方法:高斯模糊
- 变化大的区域就是边缘、点、角
- 描述特征点
- HoG,在1.2中找出的特征点为中心选16x16的区域
- 又可以分为4x4个子区域,每个子区域都可以积算一个梯度,8个bin里
- 一共是4x4x8=128维的特征向量
2. Details
找出特征点
目的是去掉一些不重要的细节。方法:高斯模糊,不同的level
不断resize,变成金字塔形状,不同的octaves。每次resize之后都高斯模糊。
建议的值octave=4,level=5
- 生成Difference of Gaussians (DoG),变化大的区域就是边缘、点、角
这是对Laplacian of Gaussian (LoG) 的一个近似
- 好处:LoG不具有尺度不变性,而DoG有
- 坏处:引入了其他的常量k,但不影响特征点位置,所以无所谓
确定极大点、极小点
粗略估计,如果在3层,27个点中是最大或最小的,就作为极值点。注意:最低或者最高层不做,因为没有相邻的三层。得到的点就是关键点
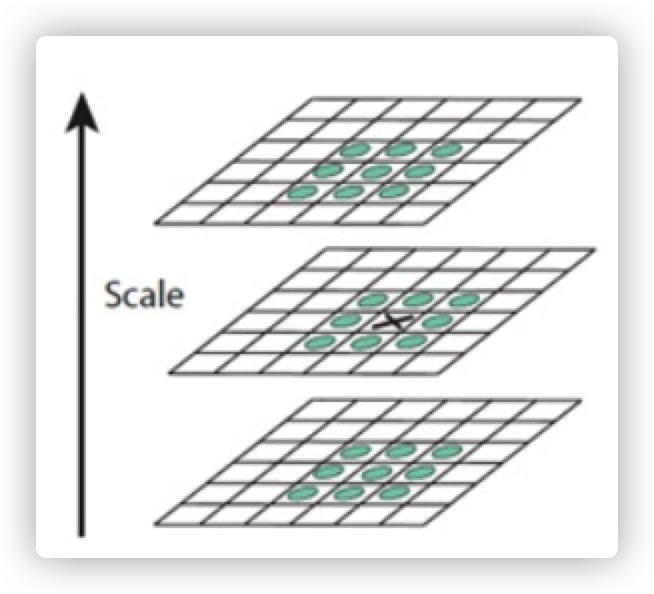
利用差分图计算亚像素,可以更精确
$$
D(\mathbf{x})=D+\frac{\partial D^{T}}{\partial \mathbf{x}} \mathbf{x}+\frac{1}{2} \mathbf{x}^{\mathrm{T}} \frac{\partial^{2} D}{\partial \mathbf{x}^{2}} \mathbf{x}
$$描述特征点
HoG,在1.2中找出的特征点为中心选16x16的区域
又可以分为4x4个子区域,每个子区域都可以积算一个梯度,8个bin里
一共是4x4x8=128维的特征向量