1. Behavior
Use control theory to describe the problem
We need a model
$$
\dot x=u
$$We need 2 basic behaviors
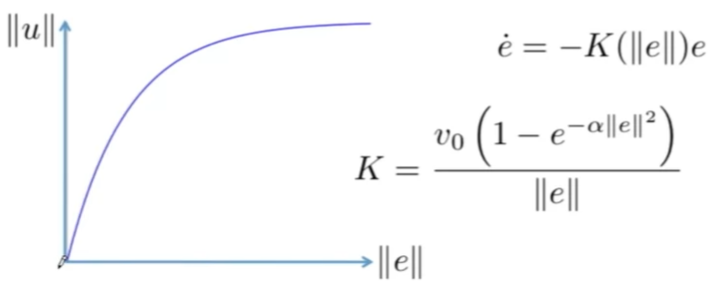
- Go-To-Goal: $e=x_g-x$, $u=Ke$, $\dot e=-\dot x=-Ke$
A concern: This is a linear controller which means the robot goes faster the further away the goal is. So in practice, make the gain $K$ a function of $e$
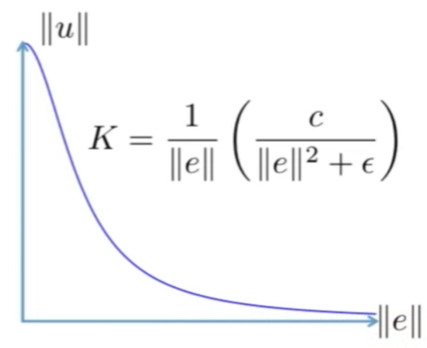
- Avoid-Obstacle:
Concern: the robot drives off to infinity, we care less the closer we get?
- Figure out the mode transitions
1.1. Hard Switch vs. Blending
This is actually a philosophical question: can robots do two thing at the same time?
Hard Switch
- Pro: performance guarantees
- Con: bumpy ride and will became Zeno problem
Blending:
- Pro: smooth ride
- Con: no guarantees
2. Boundary Following
What is convex: A set is convex if every line in-between two points in the set lies in the set
Non-Convex situation is worse!
How to follow the wall? Maintain a constant distance to the obstacle
$$
u_{FW}=\alpha R(\pi/2)u_{AO}
$$
Which direction to choose? Clockwise or Counter-Clockwise?
- No obvious answer
- Let go-to-goal behavior decide, still some issue
- When?
- How to decide $\alpha$
The Induced Mode
Design
$$
g(x)=\frac{1}{2}\left(\left|x-x_{o}\right|^{2}-\Delta^{2}\right)=0
$$
And use the induced mode method in Chapter 5 to calculate what $\dot x$ should be
In fact, the calculation give the same result as we mentioned in Boundary Following
Now the problem is that when should we stop following the wall?
3. Complete System
Enough progress $||x-x_g||<||x(\tau)-x_g)||$
- where $\tau=$ time that last switch
and clear shot to the goal
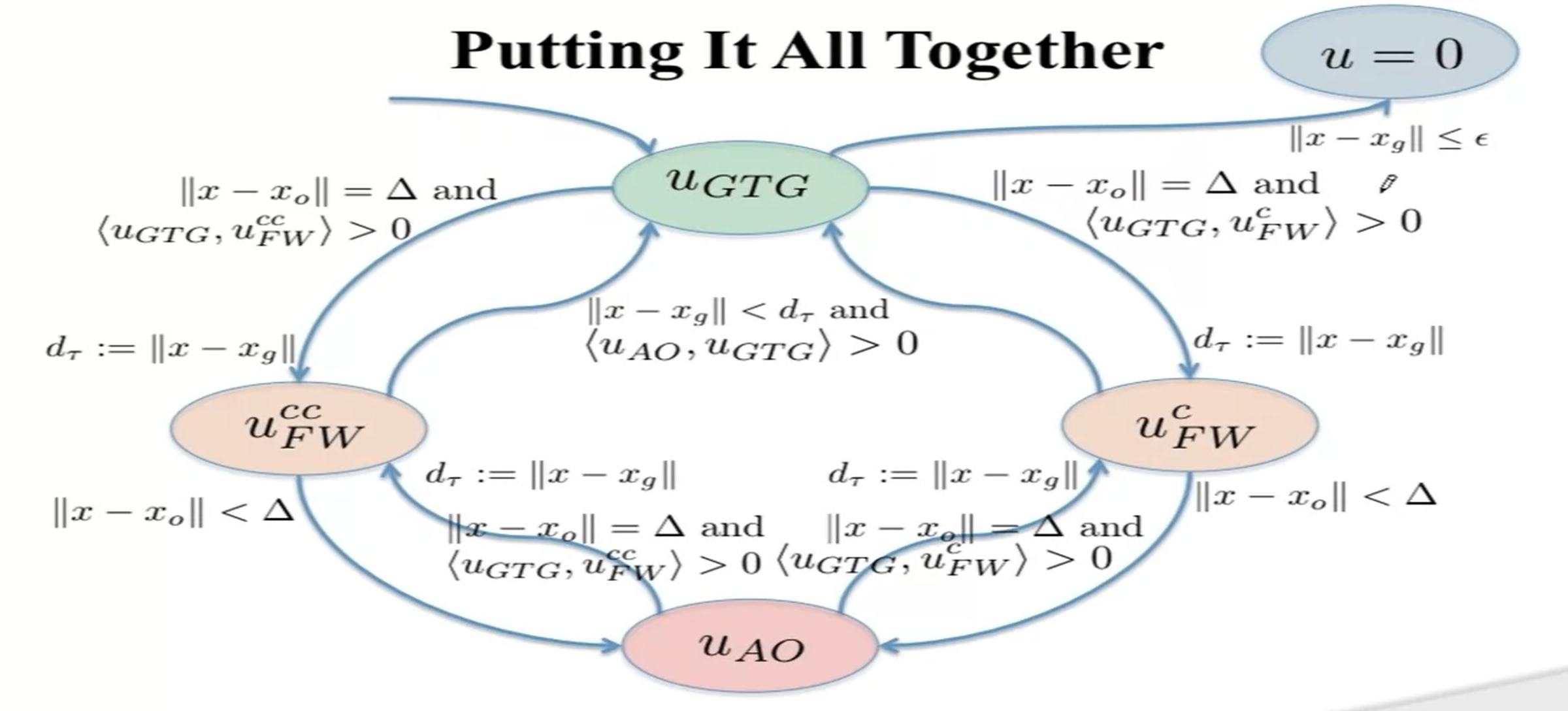
In theory, this system or framework works, however, there are some practical considerations need to be considered
- Non-Point-Obstacles
- How to define the distance to the obstacles?
- Simply the closest distance
- Weigh and add the obstacle vectors (Much better)
- Weigh and add depending on distance and direction of travel (Best)
- If we have a map, then plan (Most bestest)
- Fat Guards
- g(t) should be a line but a range
- Tweak, Tweak, Tweak the parameter