1. Switches Everywhere
Why should we switch? The robotics world is very complicated, so we should change our model and control method when situation changes.
- By necessity: the dynamics change
- By design: we want the robots to behave differently
What we are should deal with while switching?
- Model
- Stability
- Compositionality
- Traps
2. Model: Hybrid Automata
This is a finite state machine.
- Dynamics: $\dot x=f_q(x,u)$, $q$ stand for discrete state
- when $x$ is in the guard conditions, state $q$ change
- Reset the state
A Simple 2-Mode System
$$
\begin{aligned}
&\dot{x}=A_{1} x=\left[\begin{array}{cc}
-\epsilon & 1 \
-2 & -\epsilon
\end{array}\right] x\
&\dot{x}=A_{2} x=\left[\begin{array}{cc}
-\epsilon & 2 \
-1 & -\epsilon
\end{array}\right] x
\end{aligned}
$$$$
eig(A_i)=-\epsilon+1.41i
$$Both two system is stable.
Now we combine them with a hybrid automata
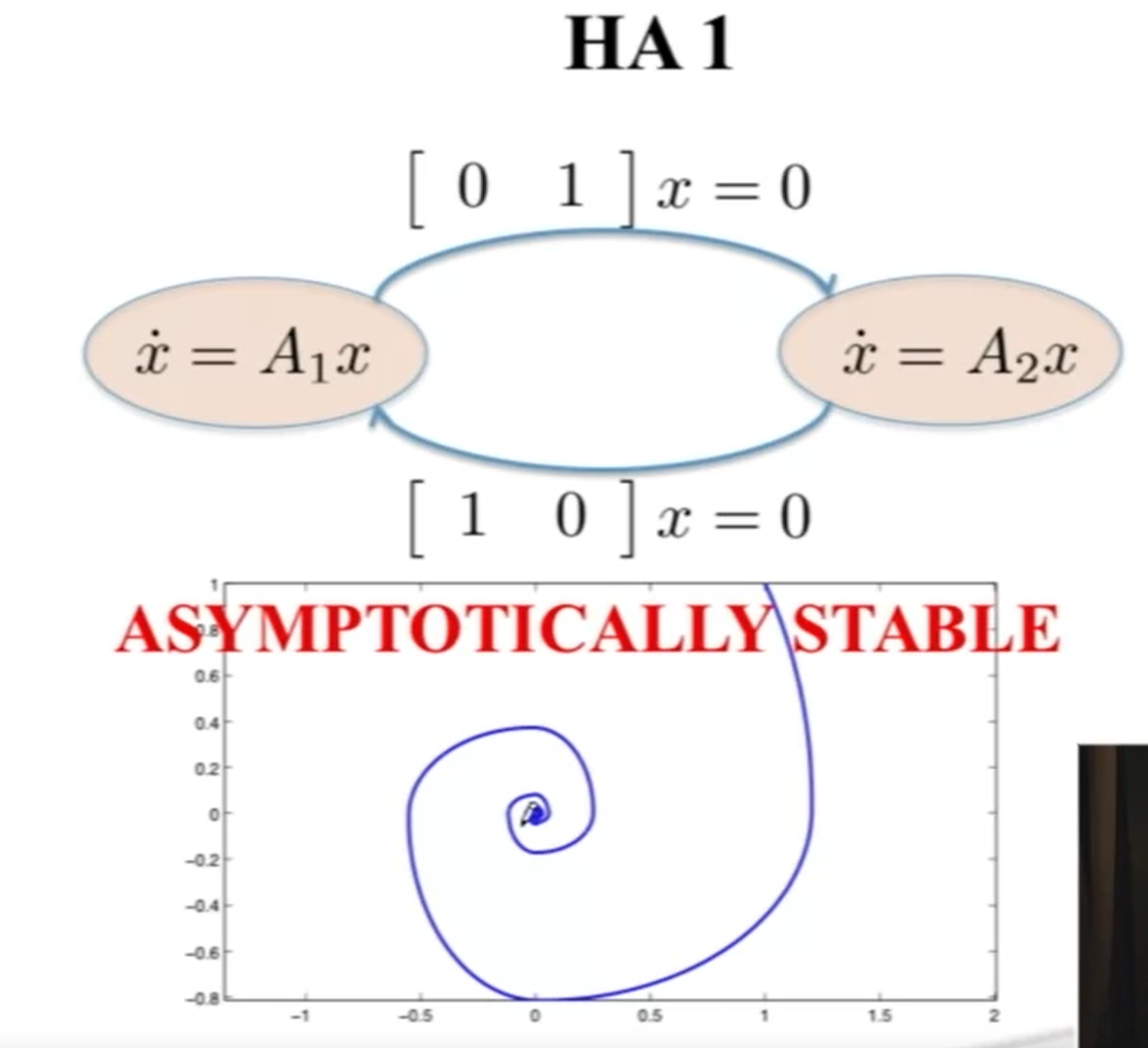
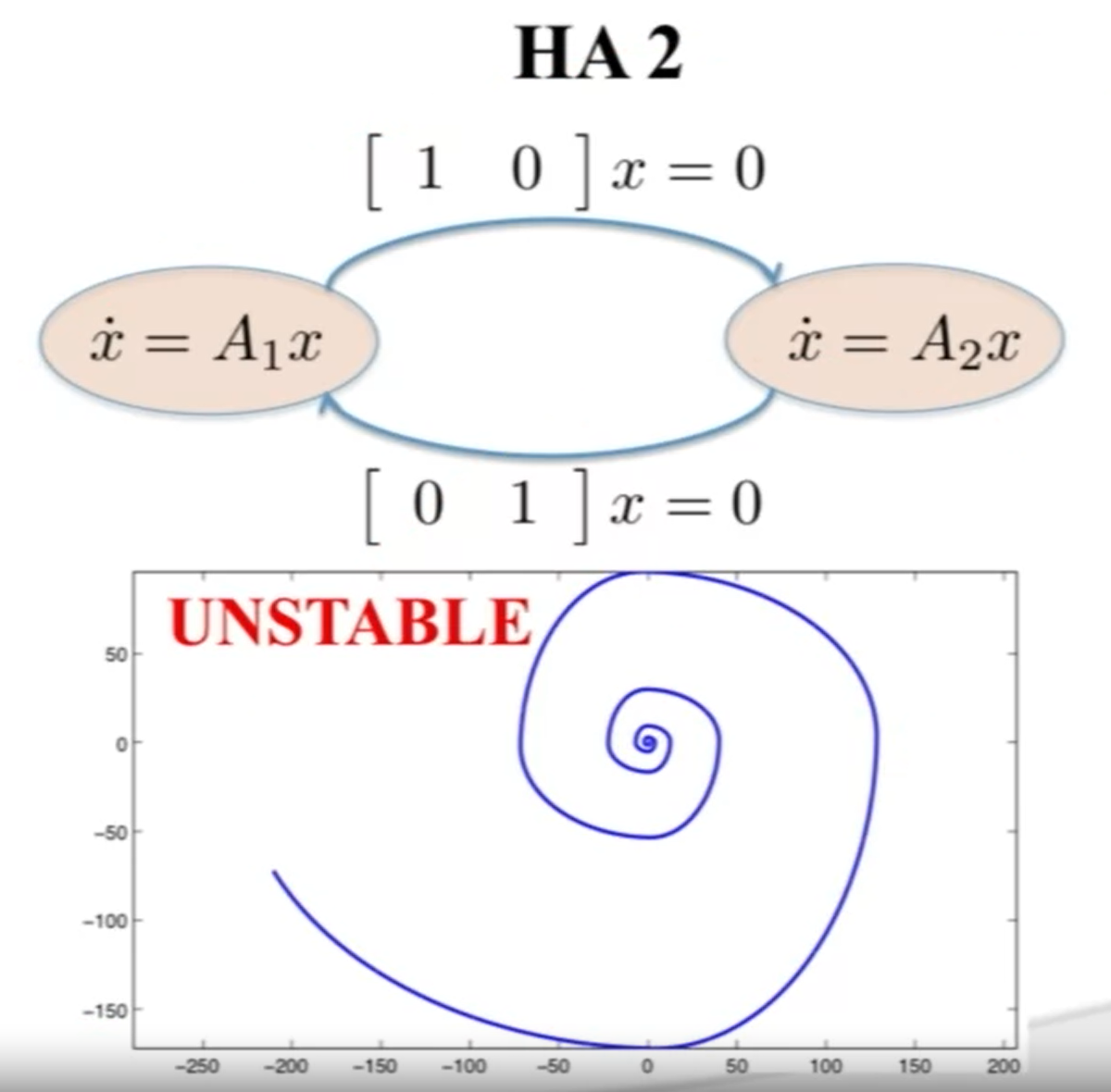
But what if we change the automata
Punchlines
- The combination of two stable modes may be unstable
3. Stability
If all the individual modes are stable, then
- Existentially Stable. Since we can pick a mode and never change
In practical, we should be aware of the potential danger and test, test, test!
4. Time Consideration
The ball bounces an infinite number of times in finite time
- Cause simulations crash
- hybrid system is undefined beyond this time
- Know as the Zeno Phenomenon
How to deal with it?
- Sliding Mode Control
A general example:
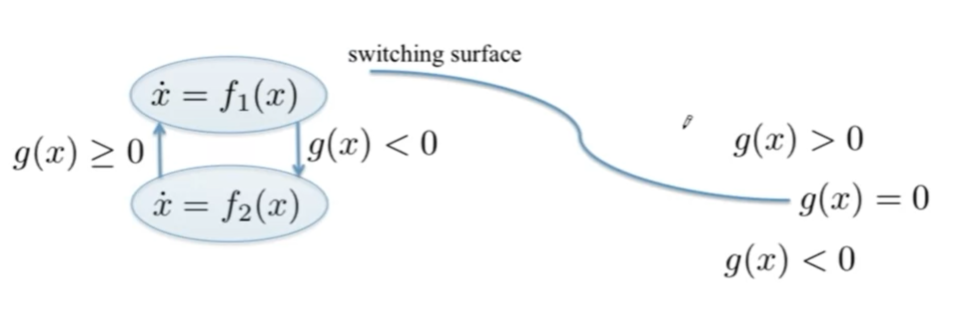We should keep sliding along the switching surface (along the line )
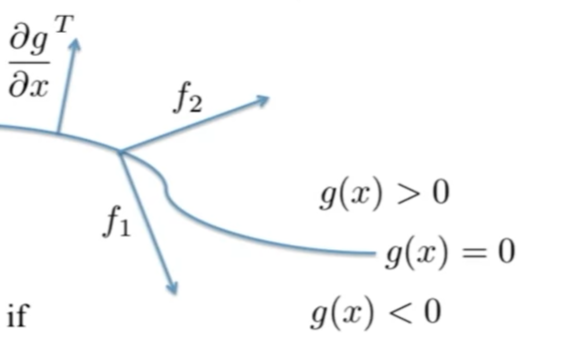
- Say this another way: $\frac{\partial g}{\partial x} f_{1}<0 \text { AND } \frac{\partial g}{\partial x} f_{2}>0$
- That means $T$ and $f_1$ / $f_2$ are in different / the same directions
Summary: Do a test, it should satisfy $\frac{\partial g}{\partial x} f_{1}<0 \text { AND } \frac{\partial g}{\partial x} f_{2}>0 $ at $g(x)=0$
5. Regularizations
What we want: $\frac{dg}{dt}=0$
$$
\frac{d g}{d t}=\frac{\partial g}{\partial x} \dot{x}=\frac{\partial g}{\partial x}\left(\sigma_{1} f_{1}+\sigma_{2} f_{2}\right)=\sigma_{1} L_{f_{1}} g+\sigma_{2} L_{f_{2}} g=0
$$
So
$$
\sigma_{2}=-\sigma_{1} \frac{L_{f_{1}} g}{L_{f_{2}} g}
$$
And we add some constraints
$$
\sigma_1+\sigma_2=1
\ \sigma_1>0
\ \sigma_2>0
$$
Design
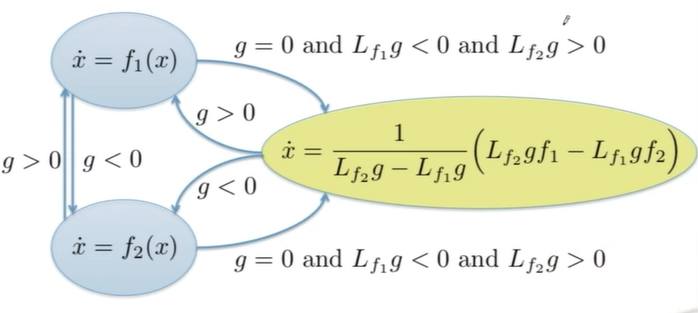
6. All in One
Type 1 Zeno: the guard condition is actually the same but flipped
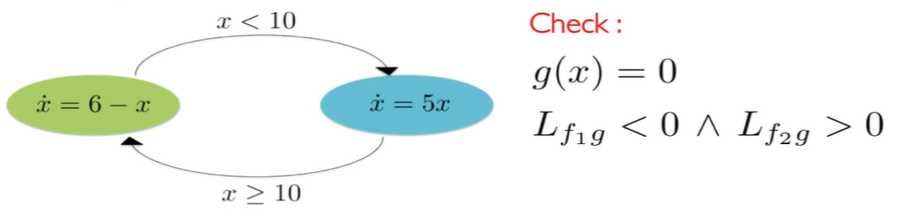
Test pass which means we must do sliding control to avoid Zeno effect