1. How to Drive Robots
We mainly need 3 part
- Controller
- Sensors
- Robot model
Some basic facts we need know
- the world is changing
- controller must be able to respond to environmental conditions
- Instead of building one complicated controller, we divide and conquer and build some Behavior
- goal-to-goal
- obstacles-avoid
- line-follow
2. Robot Model – Differential Drive Robots
This is a very common type
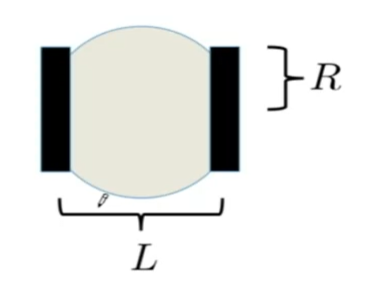
we need to know some basic parameter $L$ , $R$, easy to measure
What we can control: $v_r$ and $v_l$
What we want to control: position $x$ and $y$ and orientation $\phi$
The real input of the model is velocity of wheels $v_r$ and $v_l$. But in this way, the design of controller could be very hard, so we can translate the input to middle input form
Change $v_r$ and $v_l$ $\to$ $v$ and $w$
$$
v=\frac{R}{2}(v_l+v_r)
\
w=\frac{R}{L}(v_r-v_l)
$$
the output of the model is the state of the robot
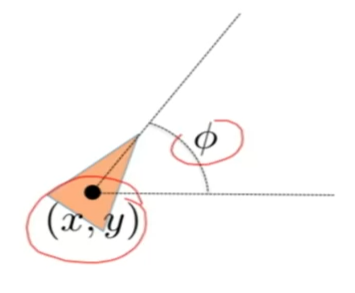
Then the physic would be simplified
$$
\left{\begin{array}{l}
\dot{x}=v \cos \phi \
\dot{y}=v \sin \phi \
\dot{\phi}=\omega
\end{array}\right.
$$
In this way, we can control the $v$ and $w$ by the controller because $v_r$ and $v_l$ could be calculated by given $v$ and $w$
3. Odometry
Two possibilities
Internal sensors
Orientation: compass
Position: accelerometers, gryoscopes
Wheel Encoders: DRIFT should be noticed

- External sensors
4. Sensor
Robots need to the world around them
standard sensor suiite, ‘SKIRT’ range
Abstraction, assume we know the distance and direction to all obstacles around us
Then, we can calculate the position of the obstacles
IR sensor: map from voltage to measured distance.
5. Behavior-Based
World is changing and unknown $\to$ Do not make sense to over-plan $\to$ develope a library of useful controller
2 Basic behavior:
- Go-to-goal
- Avoid-obstacal
6. Go to Goal
6.1. Ver.1
A Differential-drive, wheeled mobile robot
Now we want it to drive in a desired heading, how should we control $w$?
Control perspective:
- Reference: $\phi_d$
- error: $\phi_d-\phi$
- model: $\dot{\phi}=w$
Why not use PID?
$$
w=K_pe+K_I\sum ed\tau+K_d\dot e
$$
NO
6.2. Ver.2
Since the angle is something special we should consider
- Ensure that $e$ is between $[-\pi,\pi]$
- Standard strick is to use atan2
7. Obstacle Avoidance
Use the same idea by defining a desired heading
How to combine two goals?
- Winner takes all = hard switch
- Easy to analysis
- Blending = combined behaviors
- Good performance