1. Why
因为卡尔曼滤波有两个重要假设,其中的线性假设在现实环境中是不能够满足的。
大部分现实环境中的问题都包含非线性函数。如果还是使用卡尔曼滤波,那么更新状态之后就不再是高斯分布了。也就不满足卡尔曼滤波的条件了
2. How
通过泰勒展开,在均值附近线性近似。保留一阶
3. Example:传感器融合
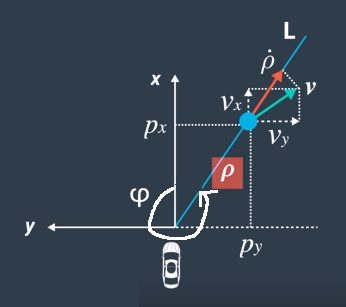
自动驾驶同时使用激光雷达和雷达两种传感器,其中
- 激光雷达:给出px,py两个
- 雷达:距离、转向、转向速度
回忆卡尔曼滤波的两个步骤
预测部分。和普通的卡尔曼滤波是完全一样的,因为这里并不涉及到观测
$$
\bar x=Fx+Bu\
\bar P=FPF^T+Q
$$
其中x是状态,P也是状态是方差(也可以理解成误差),F是状态转移矩阵,Q是过程协方差,也可以理解为在行动过程中引入的噪声,B是输入矩阵,u是系统的控制输入矫正部分。利用传感器观测到并使用贝叶斯估计计算新的状态
$ y=z-H(\bar x)$,因为我们想要的状态是在笛卡尔坐标系下的,但是观测的却是有极坐标的,因此H做了个转换
$$
h\left(x^{\prime}\right)=\left(\begin{array}{c}
\rho \
\phi \
\dot{\rho}
\end{array}\right)=\left(\begin{array}{c}
\sqrt{p_{x}^{\prime 2}+p_{y}^{\prime 2}} \
\arctan \left(p_{y}^{\prime} / p_{x}^{\prime}\right) \
\frac{p_{x}^{\prime} v_{x}^{\prime}+p_{y}^{\prime} v_{y}^{\prime}}{\sqrt{p^{\prime} 2+p^{\prime 2}}}
\end{array}\right)
$$$K=\bar P H{_j}^T(H_j\bar P H_j{^T}+R)^{-1}$
其中$H_j$是一阶雅可比矩阵
$$
H_{j}=\left[\begin{array}{llll}
\frac{\partial \rho}{\partial p_{x}} & \frac{\partial \rho}{\partial p_{y}} & \frac{\partial \rho}{\partial v_{x}} & \frac{\partial \rho}{\partial v_{y}} \
\frac{\partial \varphi}{\partial p_{x}} & \frac{\partial \varphi}{\partial p_{y}} & \frac{\partial \varphi}{\partial v_{x}} & \frac{\partial \varphi}{\partial v_{y}} \
\frac{\partial \dot{p}}{\partial p_{x}} & \frac{\partial \dot{\rho}}{\partial p_{y}} & \frac{\partial \dot{\rho}}{\partial v_{x}} & \frac{\partial \dot{\rho}}{\partial v_{y}}
\end{array}\right]
$$
所以说重点就是在矫正部分使用雅可比矩阵代替普通的H
4. Ref
https://towardsdatascience.com/extended-kalman-filter-43e52b16757d