Only Truth Matters
0%

General Path Planning (Advanced)

Posted on Edited on In , , , ,

1. Goal

Choose the most suitable path planning algorithm for mobile robot

Discrete approximation

  • Optimally efficient

Con:

  • quality depends on discretization
  • Suffer in high-dimensional spaces

1.2. Sampling-Based

No discretization

Scale well in higher dimensions

Con:

  • random lead to long computation times

2. Timeline

  • Dijkstra: 1956
  • A*: 1968
  • RRT: 1998
  • RRT*: 2010
  • Store the distance info
  • Tree would be rewired
  • CHOMP: 2013

3. Some New Algorithm

  • FMT
  • Informed RRT*
  • Narrow search space
  • Subproblem defined by a ellipse
  • BIT: find a balance between graph and sample

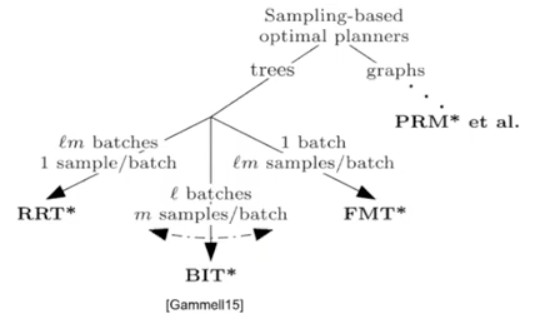
image-20230404133447946

4. BIT Algorithm

  1. Init the tree with start point
  2. Batch creation, create new sample
  3. Edge selection, processing the $Q_E$, find the best edge
  4. $Q_V$, the vertex expansion queue
  5. Edge Processing
  6. check if can improve current soluition
  7. Vertex Expansion
  8. remove a vertex from the queue and
  9. Adds outgoing edge from the vertex to the edge queue
  10. Graph Pruning
  11. remove states that cannot provide a solution better than the given cost

4.1. Ref

Python实现-BIT*-Batch Informed Tree 运动规划算法_海晨威的博客-CSDN博客

1
2
3
while self.BestVertexQueueValue() <= self.BestEdgeQueueValue():
result = self.BestInVertexQueue()
self.ExpandVertex(result)

Only expand when current point’s value is better than the point in the current tree

1
2
3
4
5
6
7
8
9
10
if (
self.g_T[vm] + self.calc_dist(vm, xm) + self.h_estimated(xm)
< self.g_T[self.x_goal]
):
actual_cost = self.cost(vm, xm)
if (
self.g_estimated(vm) + actual_cost + self.h_estimated(xm)
< self.g_T[self.x_goal]
):
if self.g_T[vm] + actual_cost < self.g_T[xm]:

Check the vvalue of a edge, should add it to tree or not

5. Problem

5.1. Empty QV

Too little sample point, increase the sample size solve the problem