Only Truth Matters
0%

RRT ROS implementation

Posted on Edited on In , , , ,

1. RRT-ROS

2. 1 RRT算法简介与实现

2.1. 1.1 基本思想

​ RRT，即rapidly exploring random tree是一种在可以高维空间中有效搜索路径的方法，它的主要思想是通过在空间中随机取点，以取样点为依据增量式扩展路径搜索树直到终点和起点都包含在搜索树中。

2.2. 1.2 伪代码

1
2
3
4
5
6
7
8
9
10
11
12
Algorithm BuildRRT
Input: Initial configuration qinit, number of vertices in RRT K, incremental distance Δq)
Output: RRT graph G

G.init(qinit)
for k = 1 to K
qrand ← RAND_CONF()
qnear ← NEAREST_VERTEX(qrand, G)
qnew ← NEW_CONF(qnear, qrand, Δq)
G.add_vertex(qnew)
G.add_edge(qnear, qnew)
return G

2.3. 1.3 代码实现

2.3.1. 1.3.1 ROS-navigation实现架构

总的来说，navigation导航包的输入是里程计和传感器数据流，输出是速度命令给机器人。

我们要修改的是其中的路径规划部分，即global_planner，只需要给出一串从起点到终点的点序列即可。

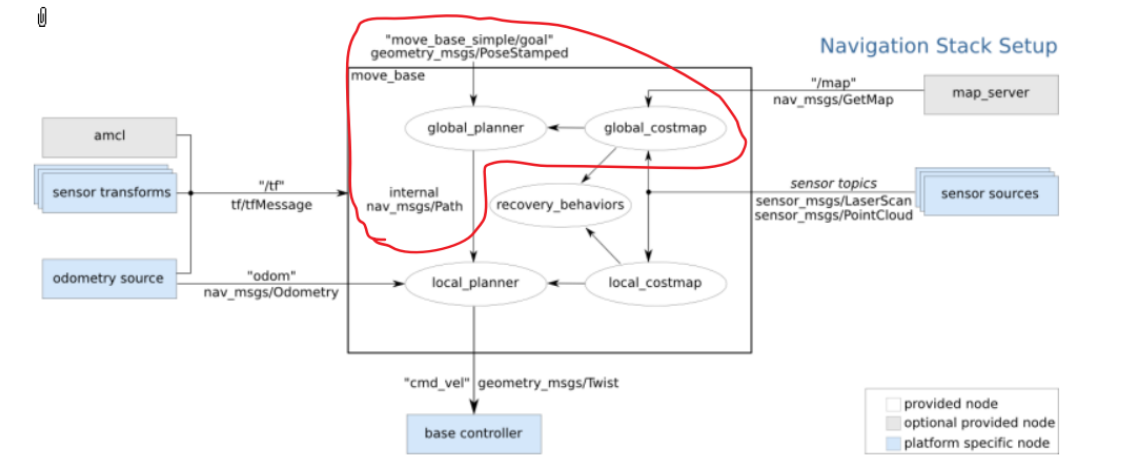
我们只需要做好其中红色线围起来的一部分，也就是说输入是起始点，终点，costmap（地图），输出是Path

2.3.2. 1.3.2 RRT-C++实现架构

思考步骤：

  1. 在planner_core.cpp中找到得到path的函数
1
2
3
4
5
if (!path_maker_->getPath(potential_array_, costmap_->getCharMap(), start_x, start_y, goal_x, goal_y, path))
{
ROS_ERROR("NO PATH!");
return false;
}

  1. 发现path_maker_ 在源程序中是GridPath(p_calc_) 或GradientPath(p_calc_)，都是输入势场，得到路径，而RRT不需要势场，所以仿照GridPath写RRT实现并修改

  2. 在rrt.h中定义rrtPlannerC类继承Traceback，在rrt.cpp中实现主体getPath函数

2.3.3. 1.3.3 RRT-C++实现思路

RRT的实现不难，要考虑的问题主要有3个：

  1. 如何进行随机采样

  • 为了使RRT具有广泛的通用性，不受障碍物的过多干扰，所以采样应尽可能多方向采样

  • 但如果采样范围太广，会使得距离最近的计算失去意义

  • 如果采样范围太小，RRT树就会只朝着几乎一个方向运动，或者让机器人在一个范围内绕圈

  • 所以我测量了有效地图的大小， 并按分辨率还原坐标

  • Xl:94.65/0.05=1893

Xr:108.90/0.05=2178

Yb:90.65/0.05=1813

Yu:101.484/0.05=2029

为了让边界的点也能被运动到，所以还要再放宽一点。最后我选择了 (1873,1793) to (2213,2053)

  1. 如何定义最近点

欧式距离，
$$
\sqrt{dx^{2}+dy^{2}}
$$

  1. 如何进行树的扩展

树的扩展是RRT算法中最重要的一部分：

  • 数据结构：树的数据结构是由定义的rrt_point组成的一维vector，其中rrt_point是一个struct，有3个变量，坐标（double x，double y）和父节点在数组中的位置（int parent）。
  • 随机采样之后，遍历树中的所有点，找到最近点，然后将不在墙中的有效随机点加入到树中，parent设为最近点的位置，这样，当最后到达终点后就能反推出一整条线路，push进path

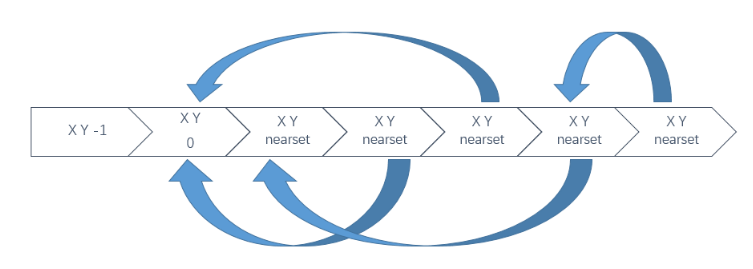
具体实现参考附件中的rrt.cpp及rrt.h中的代码及注释

3. 2 实验结果

3.1. 2.1 Dijkstra

3.2. 2.2 A*

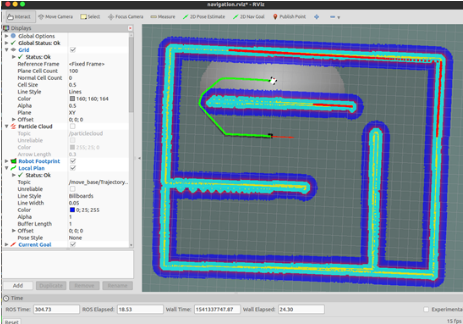
3.3. 2.3 RRT

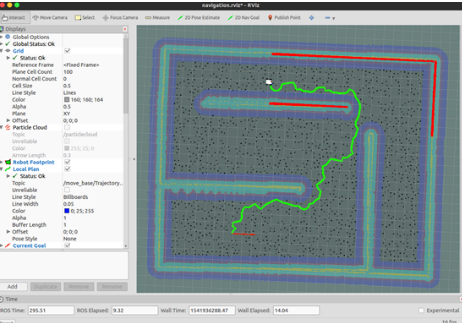
4. 3 RRT对比实验（包含改进算法）

由于单纯RRT没有利用终点和墙壁信息，所以改进算法由2部分组成

  • 利用终点，让随机采样的点更加趋向于终点，这种方法类似于人工势场法
  • 利用墙壁信息，在生成路径后将一些多余的点删除，也就是说尽量走直线，只有遇到墙时才拐弯

4.1. 3.1 概览

在本项目中，可改变的参数有4个，分别是：

变量名 含义
step 每次增加的步长
use_potential 是否使用势场法改进RRT
k 改进RRT中势能所占的比值
smooth 是否使用算法减少路径中无用的点，达到光滑效果

4.2. 3.2 实验设计

路径规划算法所要考虑的主要是时间以及距离。

  • 时间可以通过ROS的计时工具得到
  • 距离可以通过点的数量来计算（因为两点之间的距离都是step）
  • 如果使用smooth，则距离通过勾股定理计算距离和

所以我的实验步骤如下：

  1. 考察step值对算法的影响
  2. 考察potential势场法对算法的影响
  3. 考察不同k值对改进算法的影响
  4. 考察smooth对算法的影响

4.3. 3.3 实验过程

4.3.1. 3.3.1 考察step值对算法的影响

step 效果 用时(s) 距离 采样点
1 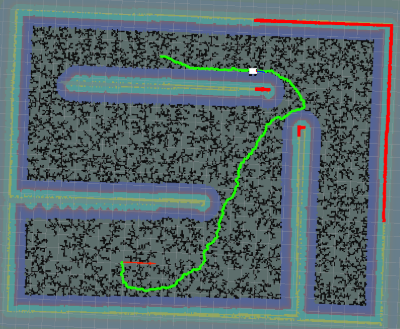14.082 408 12623
3 0.134 348 388
7 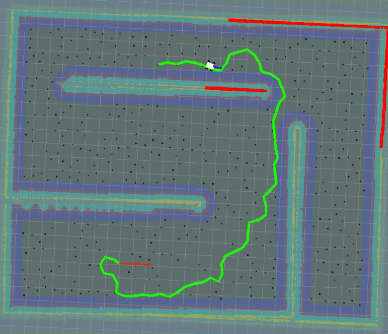0.149 420 470
15 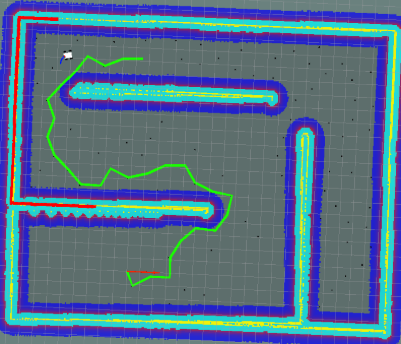0.175 420 100

通过对比可以发现，step的选择应该要适中

  • 如果step太小，会耗费大量的时间，实时性非常差
  • 如果step太大，路径的扩展步子太大，就有可能如7、15这样的情况，在终点处有超过终点的意思，造成距离的增加
  • 适当的step不仅耗时少，距离也短

4.3.2. 3.3.2 考察potential势场法对算法的影响（k=0.8）

地点 普通 势场
1
2

通过相同地点的不同算法可以看出，由于势场法加入了终点的信息，所以在路径生成的过程中更加平坦。

  • 优点：

  • 路径平坦

  • 距离更短

  • 缺点

  • 当起点与终点中存在墙时，采样的点更加多，因为大量点由于被终点吸引而进入墙中而导致的

  • 总结：

适合于路径弯折不多的情况

4.3.3. 3.3.3 考察不同k值对改进算法的影响

k值 效果 算法计算时间 距离(绿线) 采样点数
0.1 0.273 321 1003
0.5 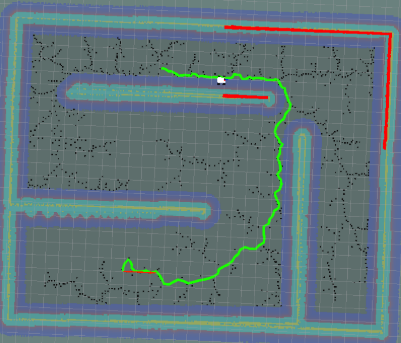0.258 357 1048
0.8 0.107 426 862
1.0 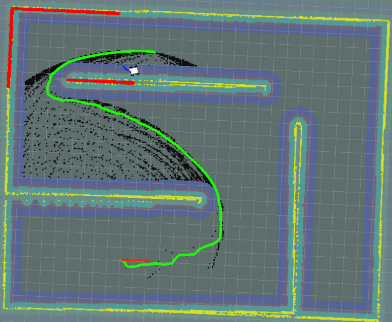16.161 1002 10272
1.0 1.431 213 4965

对比可以发现，k值的选择同样很tricky

  • 如果k太小，则几乎没有效果
  • 如果k太大，则会在一些特殊情况下造成采样点的大量增加
  • 如果k适中，则能够使路径更加平滑，更加趋向于最短距离

4.3.4. 3.3.4 考察smooth对算法的影响

算法 效果 时间 距离 点数
RRT 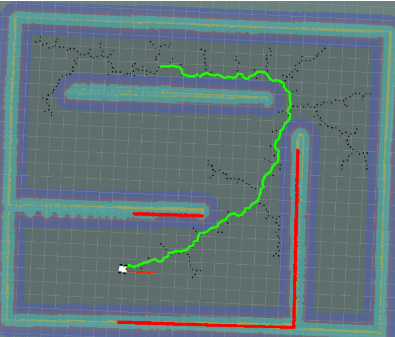0.134 348 388
potential 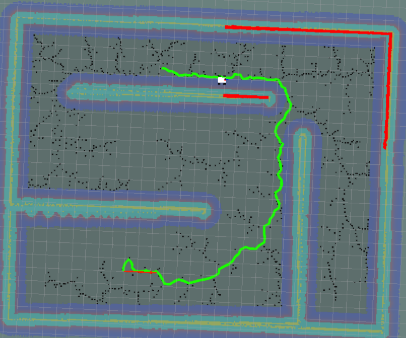0.258 357 1048
smooth 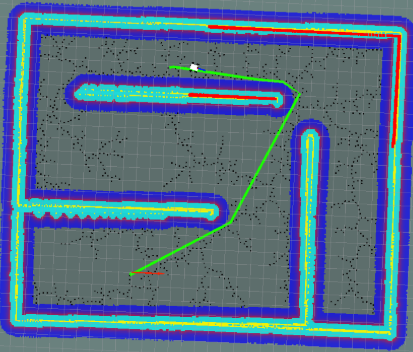0.1700 300 1061

通过对比可以看出，使用smooth可以减少距离，大量的直线也减少了local_planner的工作量

4.3.5. 3.3.5 与Dijkstra、A*算法比较

算法 效果 计算用时s 实际用时s
A* 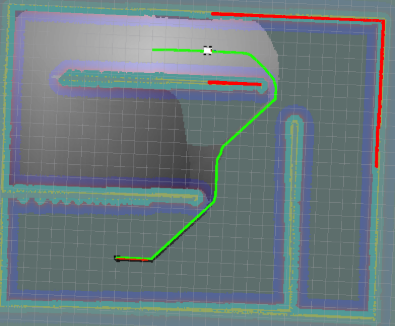0.152 85
Dijkstra 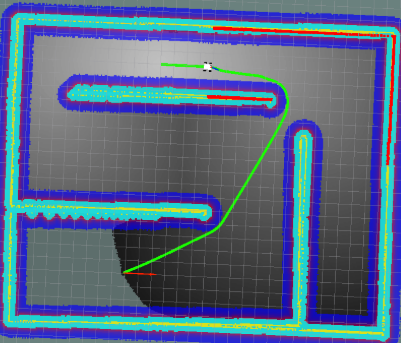0.141 90
RRT 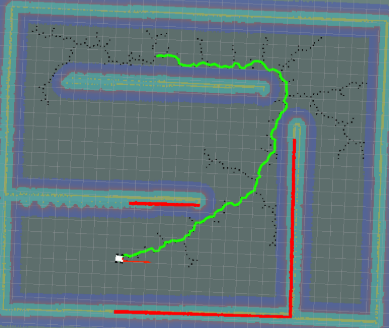0.134 89
smooth-rrt 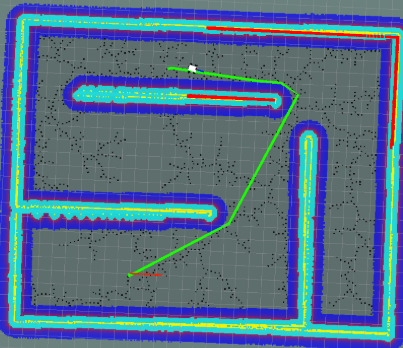0.145 93

可以看到，几种算法都没有特别显著的区别。

5. 四 结论与展望

RRT算法在全局路径规划中主要有以下优点：

  • 简单：结构简单、思想简单、实现简单
  • 易优化：非常容易加入一些额外信息来提高算法的表现
  • 通用性：RRT算法几乎在所有情况下都有不错的表现，就因为他利用了强大的扩展能力

但是也存在一些缺点：

  • 不是最优解：由于只是随机的扩展，所以RRT和最优扯不上什么关系
  • 没有在扩展时充分利用信息。如：终点位置、墙壁位置等，如果都考虑的话，就用不着RRT了

可以说，RRT可以作为在较为复杂地图中的默认路径规划算法，虽然没有最优的表现，但是经过简单优化也能有不错的表现，可以作为和其他算法对比的基准。

6. 参考文献

https://en.wikipedia.org/wiki/RRT

http://msl.cs.uiuc.edu/rrt/

[Incremental Sampling-based Algorithms for Optimal Motion Planning][Steve Lavalle]

http://wiki.ros.org/navigation/

http://wiki.ros.org/global_planner?distro=indigo