Only Truth Matters
0%

Gilbert-Johnson-Keerthi Distance Algorithm

Posted on Edited on In , , , ,

1. What

Collision Testing algorithm

  • Very general, works with any combination of convex shape
  • Fast

Useful in physics simulation and video games

2. Math Foundations

Define a shape

  • A set of points that are infinitely dense

Define the intersection: share at least one point, vector difference is 0

  • if a=b
  • then a-b=0

If there are infinite number of points, it fails

2.1. Minkowski Sum

Sum of two shape, a shape travel along another shape’s outliers

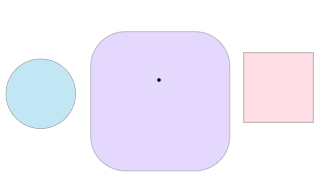
image-20230328213559449

Blue + Pink= Purple

The center is located at the sum of the original shape center

2.2. Minkowski Difference

Just like the sum, but the position are define as differences rather than sum

Key point:

  • When the shape intersect, the difference always contains the origin

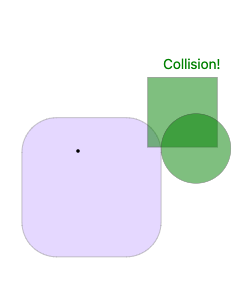
image-20230328214716877

Takeaway: We only need to test if the origin is in the Minkowski difference

2.3. Simplify

Instead of working with infinite points, we find useful points and calculate the difference of these points

The convex hull is a good approximation of the entire difference

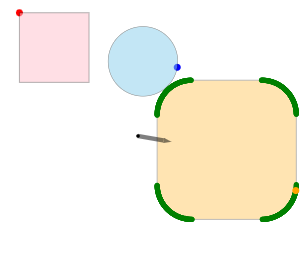
image-20230328220242147

3. Algorithm

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
Initialization:

1. Pick an arbitrary starting direction.

2. Find a point in the Minkowski difference using the support function.

3. Add this point to a Simplex, a shape created using the minimum number of
points in a given dimension. For example, a point in 0 dimensions, a
line in 2, a triangle in 3, and a tetrahedron in 4.

These shapes are easy to test for intersection, so we will find simplex
subsets of the convex hull and perform the intersection tests on them.

Main Loop:

4. Choose a new direction from the simplex towards the origin.

5. Get a point with the support function using the direction.

6. If the point didn't pass the origin, then the origin must be outside the
convex hull. Terminate and return false.

7. Add the new point to the simplex.

8. Test to see if the origin intersects the simplex.

If it does, keep the entire simplex.

If it does not, reduce to the closest, largest simplex that surrounds
the origin when it is mapped onto the simplex's dimension.

9. If we found a simplex of the maximum dimension that surrounds the origin,
terminate and return true. Otherwise, return to step 4.

Keypoint:

  • preserve the nearest K point to the origin
  • maintain a K+1 dimension simplex
  • support point calculation is important

Determine if the dot product of the new point and the last direction

  • if <0, means in the opposite direction, no hope, just exit and return false
  • if >0, mean in the same direction, should be iterate