1. 1 概论
大多数生产过程的效益取决于控制的好坏,因此控制很重要。
大多数过程可以分解为一些基本环节,掌握这些环节之后我们就可以进行改造、控制,并预估性能。
总目标:对于任意外部干扰$DV$,通过调节操作变量$MV$,使被控变量$CV/PV$维持在设定值$SP$
2. 2 过程动态特性
不同的过程动态特性不相同。
2.1. 2.1 典型动态特性,机理建模
自衡过程–纯滞后、单容、多容
非自衡–积分、指数
常用方程
- 物料守恒,能量守恒
2.2. 2.2 变送环节与控制阀特性
变送环节一般可表示为一阶+纯滞后,希望滞后和时间常数尽量小
测量信号往往会经过处理:周期性脉动、噪声–低通滤波,线性化处理–$\sqrt{x}\to x^2\to x$
控制阀直接与介质接触,工作在恶劣环境下。要谨慎选择
- 开度$15 % - 85 %$
- 气开、气关,主要考虑失气时使生产状态处于安全状态
- 进水阀气关
- 燃料阀气开
- 流量特性
- 线性阀–常数
- 等百分比阀–先慢后快
- 快开阀–先快后慢
- 抛物线阀–先慢后快
- 流量特性选择
- 设想开环增益不变,就不用改控制器参数
- 选择非线性阀补偿其他环节的变化,使开环增益保持不变
e.g.
已知热平衡$C_1G_1(T-T_1)=\lambda G_2$
那么,控制通道的静态增益
$$
K _ { p } = \frac { \partial T } { \partial G _ { 2 } } = \frac { \lambda } { C _ { 1 } G _ { 1 } } \propto \frac { 1 } { G _ { 1 } }
$$
- 若主要扰动为$T_1$,$K_p$为常数,所以选择直流线性阀
- 若主要扰动为$G_1$,所以$K_V$要$\boldsymbol { K } _ { \boldsymbol { V } } \propto G _ { 1 }$,所以选择等百分比阀
2.3. 2.3 广义对象,经验建模法
广义对象:简化控制系统的分析与设计,将执行机构、被控对象、测量变送环节合起来当成广义对象
对象获取:一般考虑为一阶+纯滞后
- 阶跃测试法
- 阶跃响应:在稳态下快速改变输入量
- 扰动信号幅度要适宜,一般$5%-15%$
- 计算$K,T,\tau$
*$K$广义对象的输出输入比
*$T=1.5(t_{y=0.632}-t_{y=0.283})$
*$\tau=t_{y=0.283}-T$
3. 3 反馈控制
最基本、应用最广泛——单回路反馈控制
反馈不是唯一的控制方法,但是最简单、鲁棒性最好。
3.1. 3.1 性能指标
以阶跃响应的特征参数为指标
衰减比 一般$4:1-10:1$之间,保持足够的稳定裕度。不希望有振荡的就不要了
余差
偏差积分性能指标
一个综合性的指标来全面反映控制的品质
- 偏差积分IE :不能保证有合适衰减比
- 平方偏差积分 ISE :数学上处理较为方便
- 绝对偏差积分 IAE :较为常用
3.2. 3.2 PID
- P比例控制
- 输出=k*偏差+稳态工作点
- 比例度$PB=1/K_c$
$K_c$的选择是对稳定性和精度*的权衡,越大精度提高,但稳定性变差 - 缺点:存在余差,但很多场合适用(液位)
- PI比例积分控制
- 静态增益$\infty$,所以没有余差
- 因为带来相角滞后,因此稳定性变差,所以$K_c$要相应减小
- 积分饱和问题:控制器的饱和输出比执行机构的范围大,使得控制信号很慢回落
- 解决方法:当发现控制器输出饱和时,就停止积分作用。用控制器的输出值作为反馈信号
- PID比例积分微分控制
- 微分控制通过误差的变化率来预报误差信号的变化趋势
- 理想微分实现不了,用传递函数近似
为什么PID在时域中有偏置$u_0$,但在复频域的算式中没有?
答:因为传递函数表达的是系统在稳态工作点附近变化时的情况
理论PID模拟算式
$$
u ( t ) = K _ { c } \left[ e ( t ) + \frac { 1 } { T _ { i } } \int _ { 0 } ^ { t } e ( \tau ) d \tau + T _ { d } \frac { d e ( t ) } { d t } \right] + u _ { 0 }
$$
当然实际上无法达到,无论是理论的积分还是微分。位置式数字PID
$$
u ( k ) = K _ { c } \left[ e ( k ) + \frac { T _ { s } } { T _ { i } } \sum _ { j = 0 } ^ { k } e ( j ) + \frac { T _ { d } } { T _ { s } } ( e ( k ) - e ( k - 1 ) ) \right] + u _ { 0 }
$$
上式计算机可以实现,但是要存储过往的误差消耗空间太大,提出增量式数字PID
$$
\begin{array} { l } { \Delta u ( k ) = u ( k ) - u ( k - 1 ) } \ { \qquad \quad= K _ { c } \left[ ( e ( k ) - e ( k - 1 ) ) + \frac { T _ { s } } { T _ { i } } e ( k ) + \frac { T _ { d } } { T _ { s } } ( e ( k ) - 2 e ( k - 1 ) + e ( k - 2 ) ) \right] } \end{array}
$$
3.3. 3.3 PID的选取与整定
选型
P:简单,调整方便,但有余差。特别适合具有积分环节的对象以及允许余差的场合
PI:大部分都是PI。流量和快速压力等滞后小、运行周期短的过程,$K_c$一般取得比较小,如果不用积分就会有较大余差
PID:对于响应过程缓慢的过程如温度控制和成分控制,可以加入微分作用。在具有高频噪声的场合不适宜PID
正反作用:
要想使得回路是负反馈,各个环节最后的乘积要为负(正作用为+,负作用为—)对象输出变大,控制器输出也变大,就是正作用参数整定
可以利用积分准则(ISE\IAE)来求最佳,但是比较费时。工程整定法如下
- 经验法
- 临界比例度法(Z-N法)
- 只保留比例作用,调整$K_c$直到系统振荡,根据临界振荡周期和临界比例增益来求PID参数
- 限制:需要对象高阶或有纯滞后,否则不会振荡
- 响应曲线法:根据一阶纯滞后模型的参数来求PID参数
4. 4 前馈控制和比例控制
反馈只有在被控变量产生偏差以后才能校正,不提供预测功能
前馈控制器
- 特点:反应快,开环控制,“专用”控制器
- 结构形式
- 静态前馈,只要稳态下实现补偿,是一个定值
- 动态前馈,即使工作点转移也能有“全补偿”的性能
- 单独的前馈不太好用,所以一般和反馈一起使用,构成前馈-反馈控制
- 对前馈来说,降低了对模型精度的要求
- 对反馈来说,对干扰做了及时的粗调
- 线性、非线性?
- 要根据系统的特性(能量守恒、物料守恒)来选择不同前馈变量之间的关系($+、 - 、\div、\times$)
其中一种特殊的方法——比值控制,工业生产中很多过程可以通过保持物料的流量比来保证产品质量
- 定比值控制
- 开环:无法保证两流量比值
- 单闭环:PI控制器,但主流量不可控,所以总流量不能控制
- 双闭环:有设定值,能控制主流量
- 变比值控制
- 干扰造成最后产品质量的误差,很难通过人工手工调节比值
- 根据工艺参数$y$自动改变比值
- 其他问题
- 实现方式
- 相乘$\times$方案:将流量作为设定值
- 相除$\div$方案:将比值作为设定值,尽量少用
- 逻辑提降:双交叉控制
5. 5 其他典型控制系统
过程变得复杂时,在单回路PID上改进
5.1. 5.1 串级控制
用途和串级类似,也是用来克服干扰。主要就是增加第二测量点,能更快检测干扰并克服。
- 主控制器接受设定值,副控制器输出控制信号
- 副回路具有快速调节作用
- 主回路对副对象有较好的鲁棒性 。因为只要副回路增益够大
- 系统设计
- 原则:
- 尽量多的干扰放在副回路中
- 副回路滞后不能太大
- 具有非线性和时变的特征放入副回路
- 控制器选型
- 主控制器PID
- 副回路大部分时候用PI
- 正反作用:反正都是要让两个回路构成负反馈
- 抗积分饱和:用负变量的测量值作为反馈信号
- 微分先行:如果给定值频繁变化,那么直接加在控制器里的微分结果会有很大的跳变。所以“先行”,加在测量变送的后面,这样就不会有跳变。
5.2. 5.2 均匀控制
要解决的问题:怎样将一个变化较剧烈的流量换成一个变化平缓的流量?
- 加一个缓冲罐,但是要增加设备、可能产生副反应
- 均匀控制:让液面平稳变化,所以相比单纯的液面控制来说,比例度宽,积分时间大
5.3. 5.3 选择控制(超驰控制)
主要用于设备软保护,也就是引入选择器,当参数达到极限时的控制手段。
设计步骤:
- 首先根据控制阀的特性确定控制器的正反特性
- 根据控制器的特性确定选择器的性质(LS\HS)
抗积分饱和:
- 限幅法:高低值限幅器
- 外反馈法(用在选择控制中):采用合适的外部信号作为反馈信号
- 当控制器1工作时,对1来说反馈信号是自己,对2来说反馈信号是外部
- 积分切除法:开环情况下自动切除积分作用
5.4. 5.4 分程和阀位控制
分程就是一台控制器操纵几个阀门。目的:
- 扩大控制阀的可调范围,改善控制系统的品质
- 有些场合可调范围特别大,所以在高低负荷下都不能好好工作,
- 选两个同向阀,组合之后,扩大可调范围
- 满足工艺操作的要求
- e.g. 有时需加热、有时又要移走热量,就要配置两个控制阀
- 设计步骤
- 根据阀的气开气关特性,选择控制器的正反作用
- 根据节能要求,确定分程区间
生产上存在多个变量都能影响同一被控变量的情况。
有良好动态性能的变量,静态性能差
e.g. 加热炉内温度可以通过两种手段改变
- 加水冷却,动态性能好,但能量损失大,静态性能差
- 改变进料多少,动态性能不佳,但静态性能好
为了协调这些矛盾,引入阀位控制
- 加水冷却回路的阀门开度要小,通过参数整定,使其动作缓慢(宽比例度、大积分时间)
- 燃料阀是普通控制
5.5. 5.5 非线性补偿方法
大多数控制过程都有一定非线性,因此要引入补偿,常用的补偿方法:
- 控制阀特性补偿:实现广义对象增益近似线性
- 串级控制
- 引入中间变量
- 变增益控制器
$pH$控制实例:
- 单回路PID控制,在$pH=7$附近容易振荡
- 带有不灵敏区的非线性PID,在$pH=7$附近控制器增益变小
- 引入非线性变化的线性PID,不用$pH$控制,而直接控制浓度
6. 6 多回路控制系统
当有多个操纵变量,多个被控变量时,如何选择输入输出就很难判断。
在设计之前,对过程的耦合程度有了充分了解之后再进行设计
6.1. 6.1 相对增益
相对增益$\lambda_{11}$为开环增益$K_{11}$(回路2开环)与闭环增益$K’_{11}$(回路2闭环)之比。
计算:
- 计算开环增益矩阵$K$,其中$K _ { i j } = \left. \frac { \partial y _ { i } } { \partial u _ { j } } \right| _ { \Delta y_ { e } = 0 }$
- 计算$\mathrm { H } = \mathrm { K } ^ { - 1 } $
- 相对增益矩阵$\left{ \mu _ { i j } \right} = \mathrm { K } \bullet \mathrm { H } ^ { T }$,其中$\bullet$为点乘,即对应位置的相乘
含义:其他通道开环时,通道$u_j-y_i$的静态增益为$K_{ij}$,当其他回路闭环时,该通道静态增益变为$\frac1{\lambda_ij}$倍
因此,相对增益越接近1越好,说明耦合越小
有了相对增益矩阵,如何进行配对?
首先接近1的先配对,然后将这一通道断开
6.2. 6.2 耦合系统中的控制器参数整定
6.3. 6.3 解耦控制方案设计
本质:设计一个计算网络,用它去抵消过程中的关联。
基于方框图的解耦器:
- 串级解耦
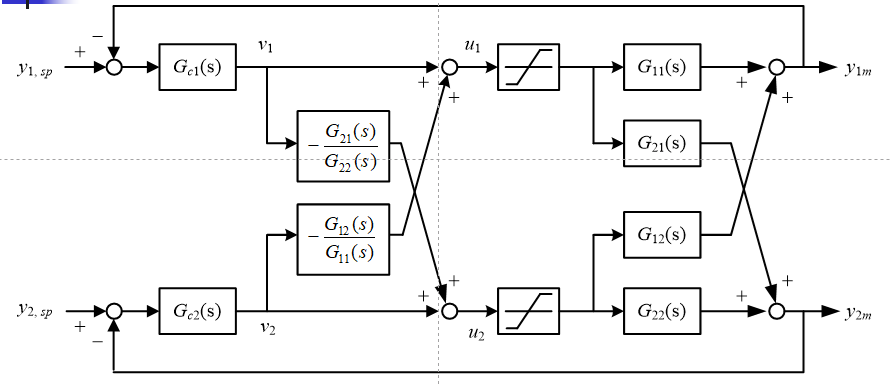
- 初始化问题,怎么样设置初值以满足无扰动地从”手动”投入”自动”?
根据$u_1,u_2$观察框图,反推$v_1,v_2$
运行约束问题,当$u_1,u_2$中有一个受到比如控制阀上下限这样地约束,就不能很好地达到控制效果。
前馈解耦
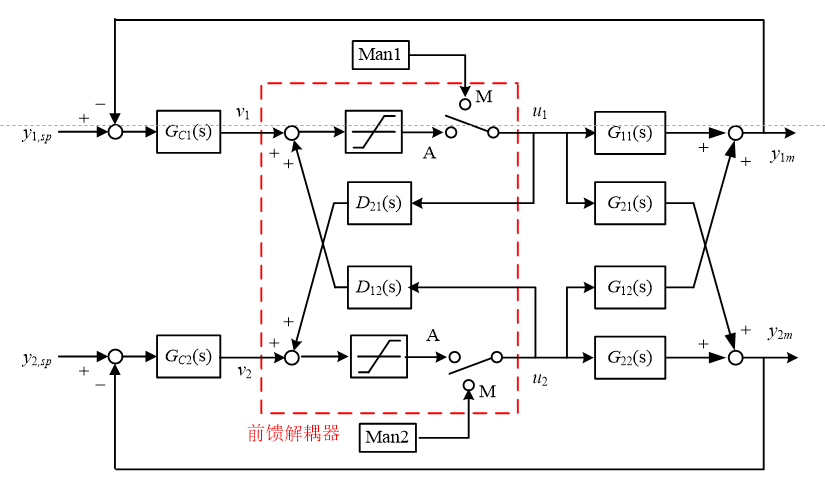
因为串级解耦的一些问题,因此工业中常用前馈解耦
- 当某一变量受约束时,使相应控制回路等价于开环
- 但是含有可能不稳定的回路
7. 7 基于模型的控制
史密斯预估器:自己进行机理建模,将纯滞后给消除掉
但是对于模型的准确度要求较高,因此改进加入预测误差滤波器$G _ { f } ( s ) = \frac { 1 } { T _ { f } s + 1 }$
8. 8 锅炉设备中汽包水位的控制
汽包水位时锅炉运行的主要指标,不能太低(容易干烧),也不能太高(容易结垢)
控制方法:
- 单冲量:只控制给水,但由于假水位现象,可能效果不好
- 双冲量:根据蒸汽流量来纠正虚假水位引起的误动作,但静态补偿比较困难,而且给水系统的干扰难以克服
- 三冲量:引入给水信号,消除给水系统的干扰
9. 9 精馏塔
9.1. 9.1 基础知识
- 单一组分液体,在封闭容器中,经过一定时间,系统达到平衡时的气相绝对压力
- 分离度$S = \frac { x _ { D } } { 1 - x _ { D } } \times \frac { 1 - x _ { B } } { x _ { B } }$
9.2. 9.2 控制问题
- 目标:控制产品纯度(大多数只有一端出料)、增加产品产率(产品量与进料的比值)
- 被控变量$CV$,产品质量、液位
- 光谱分析,可以直接得到纯度
- 相对稳定时,灵敏板温度也可以简介反映纯度
- 不稳定时,选择灵敏板温度和塔顶温度之差
- 操作变量$MV$,塔顶产品量$D$,回流量$L $
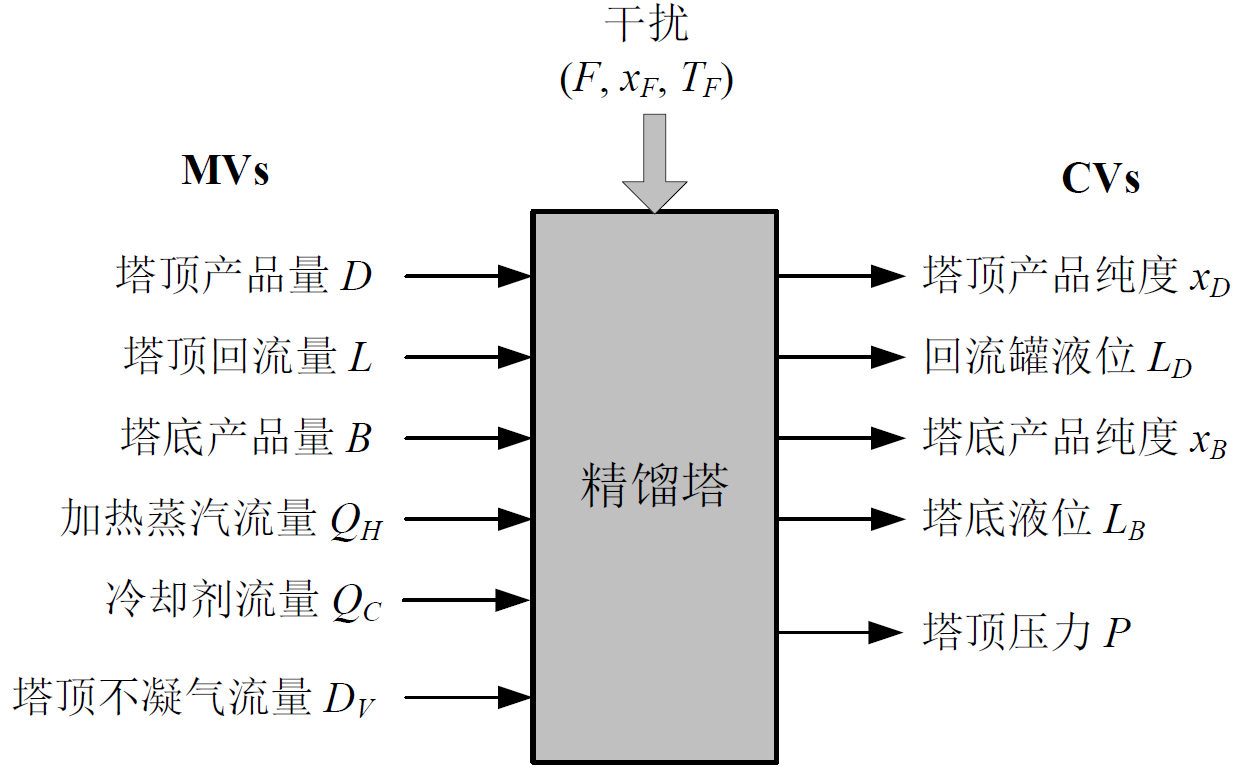
9.3. 9.3 控制方案
变量配对
就近原则:上管上,下管下
耦合程度要低
物料平衡控制
当精馏塔进料变化不大,或者纯度要求不高时,可采用纯物料平衡控制
$CV$:$L_D, L_B$顶部和底部液位
$MV$:可以用$D,L,B,Q_H$塔顶产品量、塔顶回流量、塔底产品量和加热蒸汽量
方案1:$D \to L_D$,$B \to L_B$
两液位回路无耦合
干扰因素$V$对纯度影响较大
方案2:$L\to L_D$,$B\to L_B$
两液位回路无耦合
干扰因素$V$对纯度影响较小
不适合小回流比产品
塔顶产品纯度控制
当精馏塔进料变化较大,或者纯度要求高时,可选择精馏段控制目标,塔底还是物料平衡控制
$CV$:$L_D, L_B,T_R$顶部和底部液位,塔顶产品纯度
$MV$:可以用$D,L,B,Q_H$塔顶产品量、塔顶回流量、塔底产品量和加热蒸汽量
方案1:$B\to L_B$,$L \rightarrow T _ { R} , D \rightarrow L _ { D }$
$L$对$T_R$的控制快而且强
回流量频繁波动
方案2:$B\to L_B$,$D \rightarrow T _ { R } , L \rightarrow L _ { D }$
$D$对$T_R$的控制比较慢
有利于平稳操作