Only Truth Matters
0%

PADS-Stacks

Posted on Edited on In , , ,

1. 1. Introduction to Stacks

Stacks is a kind of linear data structures.

What distinguishes one linear structure from another is where additions and removals may occur

1.1. 1.1 Stacks

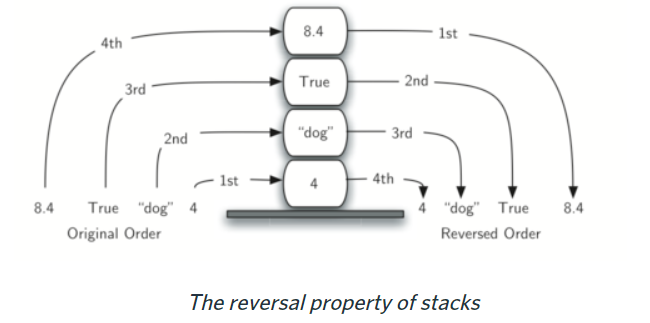
A stack is an ordered collection of items where the addition of new items and the removal of existing items always takes place at the same end.

  • Example: stack of books\plates, URL back button

  • Usage: reverse the order

stacks

1.2. 1.2 ADT

ADT data represents
DS physical implementation of an ADT
Stack operation Stack contents Return value
s.is_empty() [] True
s.push(4) [4]
s.push(‘dog’) [4, ‘dog’]
s.peek() [4, ‘dog’] ‘dog’
s.push(True) [4, ‘dog’, True]
s.size() [4, ‘dog’, True] 3
s.is_empty() [4, ‘dog’, True] False
s.push(8.4) [4, ‘dog’, True, 8.4]
s.pop() [4, ‘dog’, True] 8.4
s.pop() [4, ‘dog’] True
s.size() [4, ‘dog’] 2

2. 2. A Stack Implementation

In practice , “use a Python list as a stack”

even though the implementations are logically equivalent, they would have very different timings when performing benchmark testing.

Here, just use python list with limit function.

3. 3. Example:Balanced Parentheses

parentheses are used to order the performance of operations

$$
(5+6)×(7+8)/(4+3)
$$

or lisp function

1
2
(defun square(n)
(* n n))

So,it’s important to differentiate between parentheses that are correctly balanced and those that are unbalanced in strucures.

  • Why Stack ? open match close\ close match open, reverse order
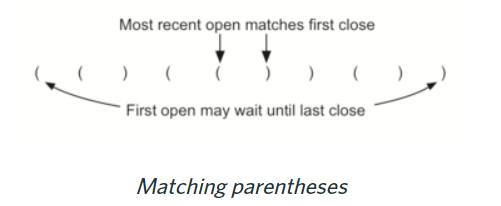
  • parentheses
  • So a stack, push if open, pop if close. Finally, if len(stack)==0, balance.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
PAIRINGS = {
'(': ')',
'{': '}',
'[': ']'
}


def is_balanced(symbols):
stack = []
for s in symbols:
if s in PAIRINGS.keys():
stack.append(s)
continue
try:
expected_opening_symbol = stack.pop()
except IndexError:  # too many closing symbols
return False
if s != PAIRINGS[expected_opening_symbol]:  # mismatch
return False
return len(stack) == 0  # false if too many opening symbols


is_balanced('{{([][])}()}')  # => True
is_balanced('{[])')  # => False
is_balanced('((()))')  # => True
is_balanced('(()')  # => False
is_balanced('())')  # => False

4. 4. Example: Converting Number Bases

$$
233_{10}=11101001_{2}
$$

  • Why stack？ Divide by Base algorithm

conver-num-base

  • So, Push fisrt, Pop at the end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
DIGITS = '0123456789abcdef'


def convert_to_base(decimal_number, base):
remainder_stack = []

while decimal_number > 0:
remainder = decimal_number % base
remainder_stack.append(remainder)
decimal_number = decimal_number // base

new_digits = []
while remainder_stack:
new_digits.append(DIGITS[remainder_stack.pop()])

return ''.join(new_digits)


convert_to_base(25, 2)  # => '11001'
convert_to_base(25, 16)  # => '19'

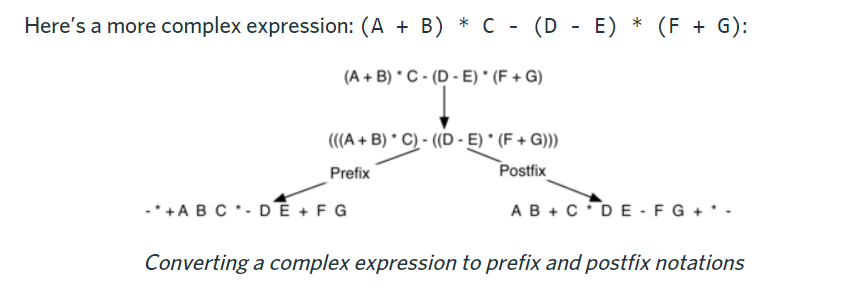
5. 5. Example: Infix, Prefix and Postfix Expressions

Infix expression Prefix expression Postfix expression
A + B + A B A B +
A + B * C + A * B C A B C * +
  • Infix expression need parenthese to force the performance of addition before multiplication.
  • Prefix & Postfixexpression DON’T need it

How to convert infix to prefix or postfix?

Fully parenthesize the expression using the order of operations. Then move the enclosed operator to the position of either the left or the right parenthesis depending on whether you want prefix or postfix notation.

postfix

5.1. 5.1 Algorithm

  1. Create an empty stack called operation_stack for keeping operators. Create an empty list for output.
  2. Convert the input infix string to a list by using the string method split.
  3. Scan the token list from left to right.
  • If the token is an operand, append it to the end of the output list.
  • If the token is a left parenthesis, push it on the operation_stack.
  • If the token is a right parenthesis, pop the operation_stack until the corresponding left parenthesis is removed. Append each operator to the end of the output list.
  • If the token is an operator, *, /, +, or -, push it on the operation_stack. However, first remove any operators already on the operation_stack that have higher or equal precedence and append them to the output list.
  1. When the input expression has been completely processed, check the operation_stack. Any operators still on the stack can be removed and appended to the end of the output list.

5.2. 5.2 Implementation

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
PRECEDENCE = {
'*': 3,
'/': 3,
'+': 2,
'-': 2,
'(': 1
}

CHARACTERS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
DIGITS = '0123456789'
LEFT_PAREN = '('
RIGHT_PAREN = ')'


def infix_to_postfix(infix_expression):
operation_stack = []
postfix = []
tokens = infix_expression.split()

for token in tokens:
if token in CHARACTERS or token in DIGITS:
postfix.append(token)
elif token == LEFT_PAREN:
operation_stack.append(token)
elif token == RIGHT_PAREN:
top_token = operation_stack.pop()
while top_token != LEFT_PAREN:
postfix.append(top_token)
top_token = operation_stack.pop()
else:
while operation_stack and \
(PRECEDENCE[operation_stack[-1]] >= PRECEDENCE[token]):
postfix.append(operation_stack.pop())
operation_stack.append(token)

while operation_stack:
postfix.append(operation_stack.pop())
return ' '.join(postfix)

infix_to_postfix('A * B + C * D')  # => 'A B * C D * +'
infix_to_postfix('( A + B ) * C - ( D - E ) * ( F + G )')
# => 'A B + C * D E - F G + * -'
infix_to_postfix('( A + B ) * ( C + D )')  # => 'A B + C D + *'
infix_to_postfix('( A + B ) * C')  # => 'A B + C *'
infix_to_postfix('A + B * C')  # => 'A B C * +'