1. 1. 目标
- 问题描述
- 数据分析
- 中间结果分析
- 结果讨论
- 缺点认识
2. 2. 问题描述及数据定义
2.1. 2.1 问题描述
利用KNN算法对iris数据集进行分类,并用训练集的训练结果对测试集进行预测,观察预测效果。
因为数据集是有标签的,所以这是一个典型的有监督分类问题
2.2. 2.2 数据定义
数据来源:UCI
iris数据集中共有3个种类的花,每种花各有50个样本:
- 其中一个样本与另外两个样本线性可分
- 其中另一个样本与另外两个样本线性不可分
每个样本各有4个属性(x):
- sepal length in cm
- sepal width in cm
- petal length in cm
- petal width in cm
预测结果一共有3种:
- setosa
- versicolor
- virginica
2.3. 2.3 计划流程
- 读取、处理数据
- 实现KNN
- 计算相似性(使用欧几里得距离)
- 计算最相近的K个邻居
- 生成预测
- 观察结果(预测准确性)
3. 3 代码实现
具体代码见notebooks/knn-iris.ipynb 或者notebooks/knn-iris.html
3.1. 3.1 读取、处理数据
首先通过读取iris.data可以得到这样的信息
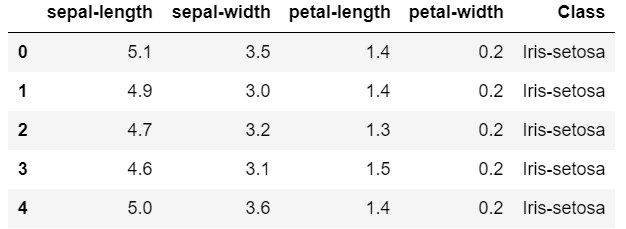
通过统计可以发现petal-length的标准差最大,猜测可能含有最多信息

为了验证算法的效果,我们将数据分成训练集和测试集,比例为4:1
之后为了排除数据大小的干扰,再将数据标准化
通过可视化可以看出在二维平面上也能大概分出3种花
3.2. 3.2 实现KNN
KNN算法有不同的形式
- 无监督学习:
- 聚类
- 有监督学习:
- 标签离散:分类
- 标签连续:回归
我们在这里要实现的有监督学习下的标签离散情况,也就是分类。
K近邻分类器是一个基于样本的分类器,也就是说它并不会训练一个General的模型来预测分类,而是简单地根据样本距离来进行投票确定分类
创建一个类KNN_Classification
有以下函数
- 计算欧式距离
$d\left(x, x^{\prime}\right)=\sqrt{\left(x_{1}-x_{1}^{\prime}\right)^{2}+\left(x_{2}-x_{2}^{\prime}\right)^{2}+\ldots+\left(x_{n}-x_{n}^{\prime}\right)^{2}}$
- 要注意向量长度,不要将标签值也计算进距离中
- 可以调用numpy来提高运算速度
- 计算获取最近邻
- 输出预测结果
3.3. 3.3 预测结果
因为在KNN算法中只有一个K值是可以改变的变量,因此我改变K值来观察预测效果,但是发现预测结果会不断变化。
测试条件:K取1-90
大部分情况下预测精度随K值的变化规律是这样的
也就是说随着K值的增大,预测精度是不断降低的。
但是在测试过程中也出现过以下情况的变化规律
这种情况比较反常,也即是K稍大时预测结果较好,K偏小或偏大时效果都不佳。
4. 4 分析
4.1. 4.1 异常测试结果分析
在3.3 中出现的问题,经过分析我认为是以下原因造成的
- 样本较少。因为一共只有150个样本,还有分成训练集和测试集,所以效果不好。
- 随即采样。对于有着很多样本的数据来说,这样采样方式可能没有什么问题,但是因为这个数据集样本太少,导致采样结果不再能反应数据的真是分布。
- KNN算法的原理。自己实现过KNN之后我发现,其实对于KNN算法来说,分成测试集和训练集的意义和一般的机器学习算法不同:KNN的模型就是数据本身(训练集),所以数据的多少和分布是否有效(能代表真实分布)会很大程度上影响预测效果。所以因为前两点原因加上KNN自身的算法,导致了预测结果的不稳定
4.2. 4.2 K值选取
在KNN算法中,K是唯一一个超参数(hyper parameter),因此要想达到好的预测效果,选择一个合适的K是非常重要的。
从图像上看,K控制的是分割平面的边界。比如说当K较小时,这个区间就会较小,直观上理解就是K仅仅观察临近的几个样本,而没有全局意识,哪怕它的旁边有一个异常点,它也把异常当成同类
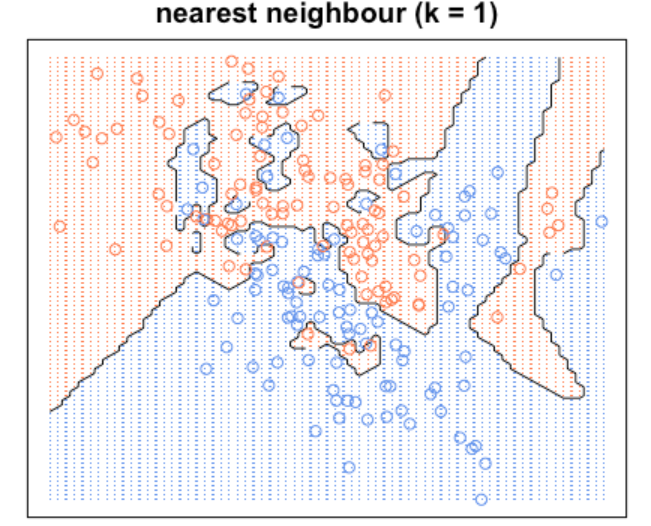
另一方面,当K较大时,预测值更加关注的是全局的情况,所以这时它就会忽略一些异常值,这使得边界更加平滑
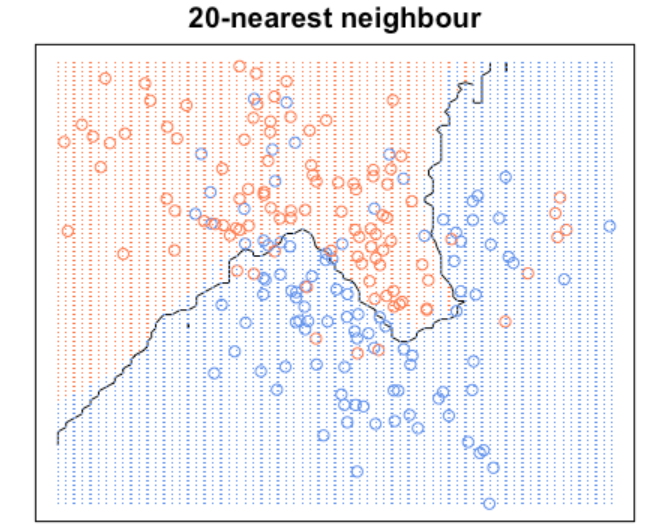
4.3. 4.3 KNN算法的优缺点
优点:
- 容易理解,容易实现(核心代码不足百行)
- 计算速度快,最耗时的操作也不过是计算距离
- 适用于多分类问题
缺点:
- 对数据集要求较高,在合适的数据集(样本量大,分布均匀,样本平衡)上能狗取得不错的效果,但是一旦数据集不佳,效果会大打折扣
- 在维数较高的场合效果不佳,因为计算的是欧氏距离,所以距离是平方和,因此无法体现出各个维度的区别
4.4. 4.4 改进方法
- 使用不同的相似性度量,而不是简单的欧氏距离
- 在高维数据上使用时可以采用数据降维,使用PCA等算法降低维数,改善效果
- 使用K-D tree等方法存储数据,减小计算量
5. 5 总结
在这个项目中,我学习了KNN算法,包括它的工作原理和如何编写KNN算法、如何使用KNN算法。我使用KNN算法对iris数据集进行测试,得到的效果还不错。
6. 参考资料
A Complete Guide to K-Nearest-Neighbors with Applications in Python and R
Tutorial To Implement k-Nearest Neighbors in Python From Scratch